Repeated Summary Traditional
Source:vignettes/RepeatedSummaryTraditional.Rmd
RepeatedSummaryTraditional.RmdThis page examines a single-factor within-subjects (repeated measures) design using summary statistics input, focusing on omnibus and pairwise analyses.
Preliminary Tasks
Data Entry
This code inputs the variable summaries and creates a summary table.
Outcome1 <- c(N = 10, M = 8.000, SD = 1.414)
Outcome2 <- c(N = 10, M = 11.000, SD = 2.211)
Outcome3 <- c(N = 10, M = 12.000, SD = 2.449)
RepeatedMoments <- construct(Outcome1, Outcome2, Outcome3, class = "wsm")This code creates a correlation matrix.
Summary Statistics
This code confirms the descriptive statistics from the summary table and matrix.
(RepeatedMoments) |> describeMoments()
Summary Statistics for the Data
N M SD
Outcome1 10.000 8.000 1.414
Outcome2 10.000 11.000 2.211
Outcome3 10.000 12.000 2.449
(RepeatedCorr) |> describeCorrelations()
Correlations for the Data
Outcome1 Outcome2 Outcome3
Outcome1 1.000 0.533 0.385
Outcome2 0.533 1.000 0.574
Outcome3 0.385 0.574 1.000 Analyses of the Omnibus Effect
The Analysis of Variance examines the overall differences among the means.
Source Table
Display the source table.
(RepeatedMoments) |> describeEffect(RepeatedCorr)
Source Table for the Model
SS df MS
Subjects 75.302 9.000 8.367
Measures 86.667 2.000 43.333
Error 40.667 18.000 2.259Proportion of Variance Accounted for
Get an estimate of the proportion of variance account for by the factor (and the confidence interval for that estimate).
(RepeatedMoments) |> estimateEffect(RepeatedCorr)
Proportion of Variance Accounted For by the Model
Est LL UL
Measures 0.681 0.389 0.772Significance Test
Test the overall differences for statistical significance.
(RepeatedMoments) |> testEffect(RepeatedCorr)
Hypothesis Test for the Model
F df1 df2 p
Measures 19.180 2.000 18.000 0.000Analyses of Pairwise Comparisons
The analyses for the pairwise comparisons do not assume homogeneity of variance and do not make adjustments for multiple comparisons (and are therefore effectively equivalent to a series of paired samples t tests).
Confidence Intervals
Obtain interval estimates for the pairwise comparisons.
(RepeatedMoments) |> estimatePairwise(RepeatedCorr)
Confidence Intervals for the Pairwise Mean Differences
Diff SE df LL UL
Outcome1 v Outcome2 3.000 0.596 9.000 1.651 4.349
Outcome1 v Outcome3 4.000 0.730 9.000 2.348 5.652
Outcome2 v Outcome3 1.000 0.683 9.000 -0.546 2.546Provide a traditional plot of the confidence intervals for the pairwise comparisons (including a line that represents no difference for the comparisons).
(RepeatedMoments) |> plotPairwise(RepeatedCorr, line = 0, values = FALSE)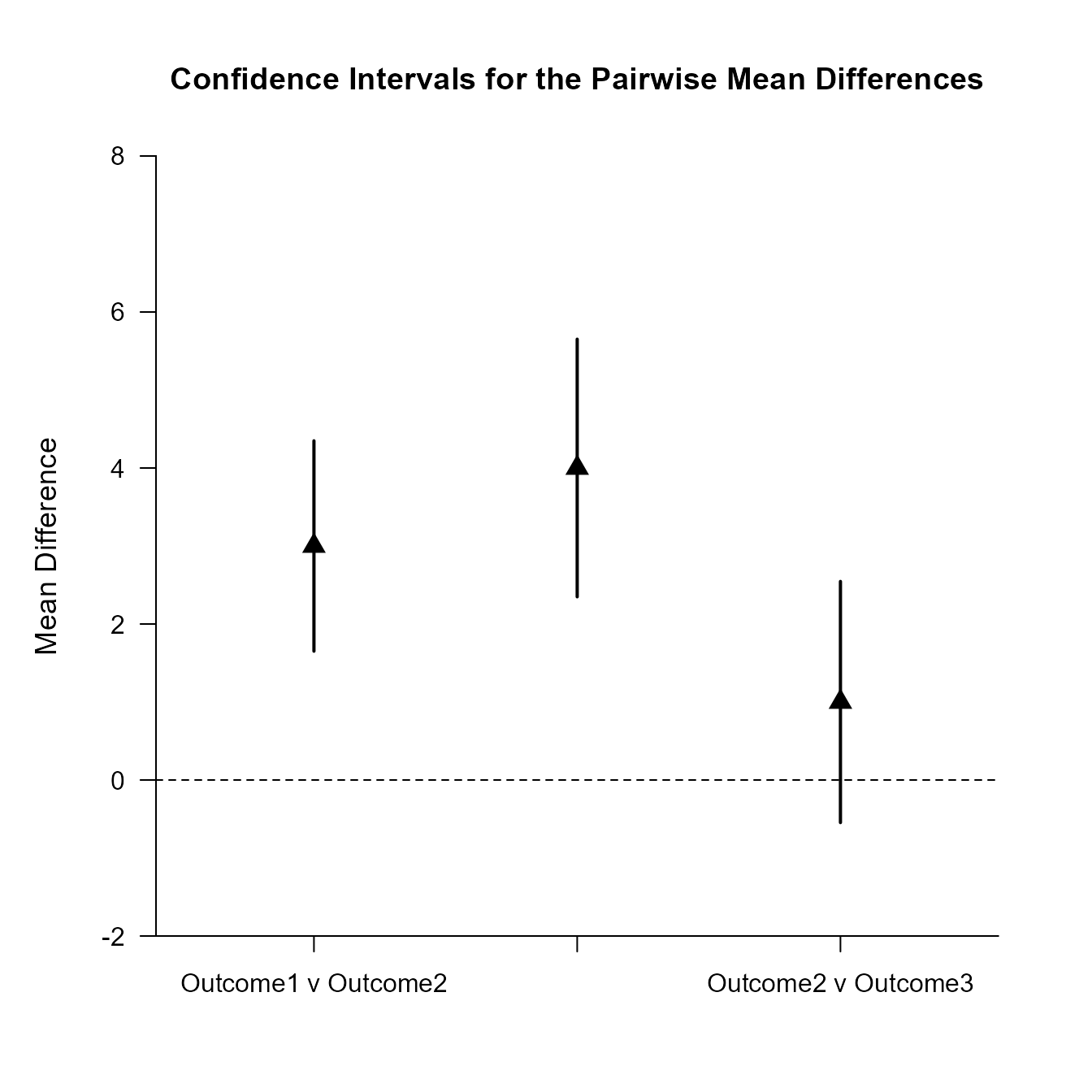
Provide a diffogram (plot of means and the confidence intervals for the pairwise comparisons).
(RepeatedMoments) |> plotPairwiseDiffogram(RepeatedCorr)
Significance Tests
Test the pairwise comparisons for statistical significance.
(RepeatedMoments) |> testPairwise(RepeatedCorr)
Hypothesis Tests for the Pairwise Mean Differences
Diff SE df t p
Outcome1 v Outcome2 3.000 0.596 9.000 5.031 0.001
Outcome1 v Outcome3 4.000 0.730 9.000 5.479 0.000
Outcome2 v Outcome3 1.000 0.683 9.000 1.463 0.177Standardized Effect Sizes
Get the standardized effect sizes (and their confidence intervals) for the pairwise comparisons.
(RepeatedMoments) |> standardizePairwise(RepeatedCorr)
Confidence Intervals for the Pairwise Standardized Mean Differences
d SE LL UL
Outcome1 v Outcome2 1.617 0.466 0.703 2.530
Outcome1 v Outcome3 2.000 0.531 0.959 3.042
Outcome2 v Outcome3 0.429 0.333 -0.224 1.082Analyses of Relational Intervals
Relational intervals are values (and boxes on a graph) that indicate whether two conditions are statistically significantly different. The analyses for the relational confidence intervals do assume homogeneity of variance but do not make adjustments for multiple comparisons.
Provide estimates of the arelational and relational intervals.
(RepeatedMoments) |> estimateRelational(RepeatedCorr)
Confidence and Relational Intervals for the Means
M RI.LL RI.UL CI.LL CI.UL
Outcome1 8.000 7.294 8.706 6.988 9.012
Outcome2 11.000 10.294 11.706 9.418 12.582
Outcome3 12.000 11.294 12.706 10.248 13.752Plot the intervals.
(RepeatedMoments) |> plotRelational(RepeatedCorr)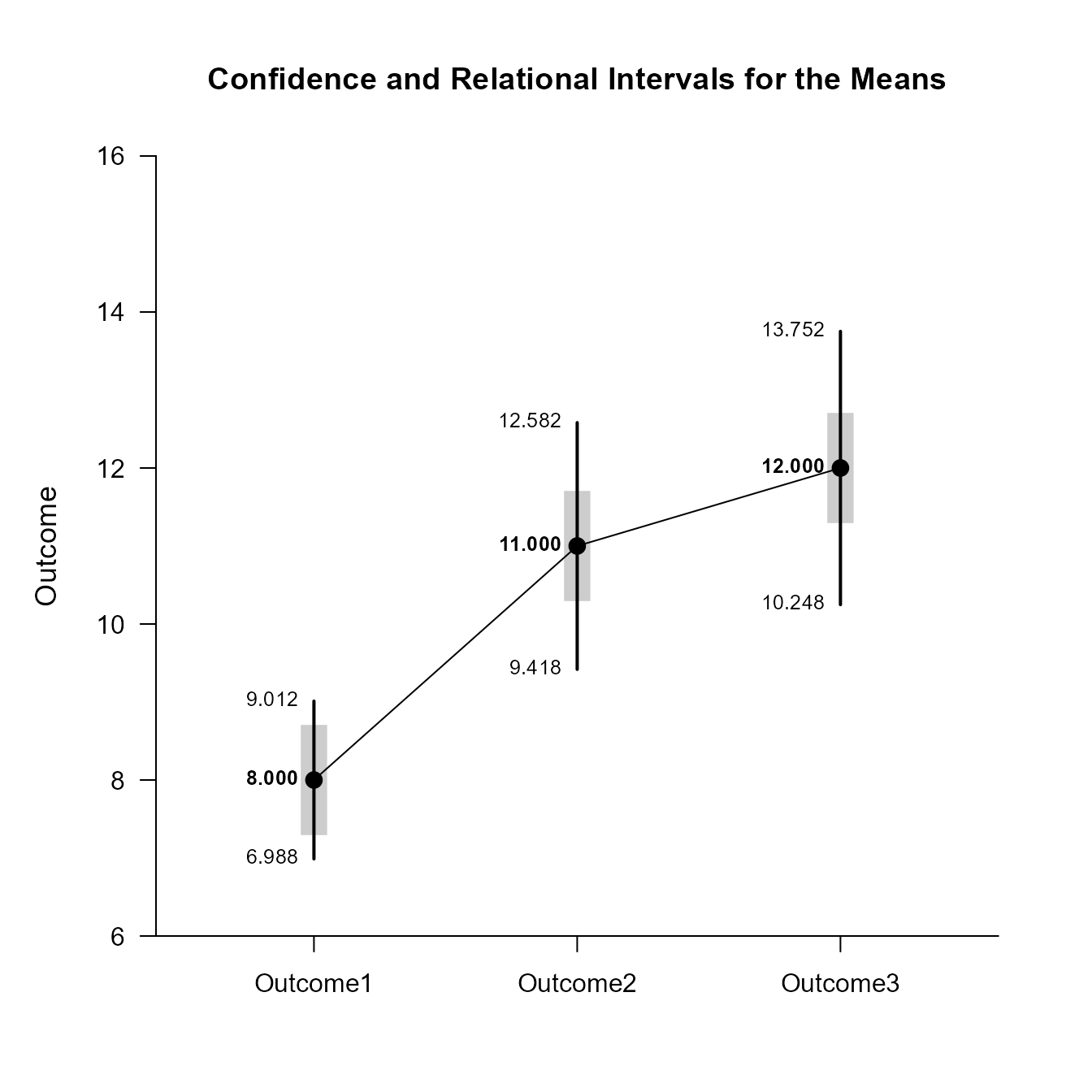
Analyses of Post Hoc Comparisons
The analyses for the post hoc comparisons do assume homogeneity of variance and do make adjustments for multiple comparisons (based on Tukey HSD procedures).
Confidence Intervals
Obtain interval estimates for the post hoc comparisons.
(RepeatedMoments) |> estimatePosthoc(RepeatedCorr)
Confidence Intervals for the Posthoc Mean Differences
Diff SE df LL UL
Outcome1 v Outcome2 3.000 0.596 9.000 1.335 4.665
Outcome1 v Outcome3 4.000 0.730 9.000 1.962 6.038
Outcome2 v Outcome3 1.000 0.683 9.000 -0.908 2.908Provide a traditional plot of the confidence intervals for the post hoc comparisons (including a line that represents no difference for the comparisons).
(RepeatedMoments) |> plotPosthoc(RepeatedCorr, line = 0, values = FALSE)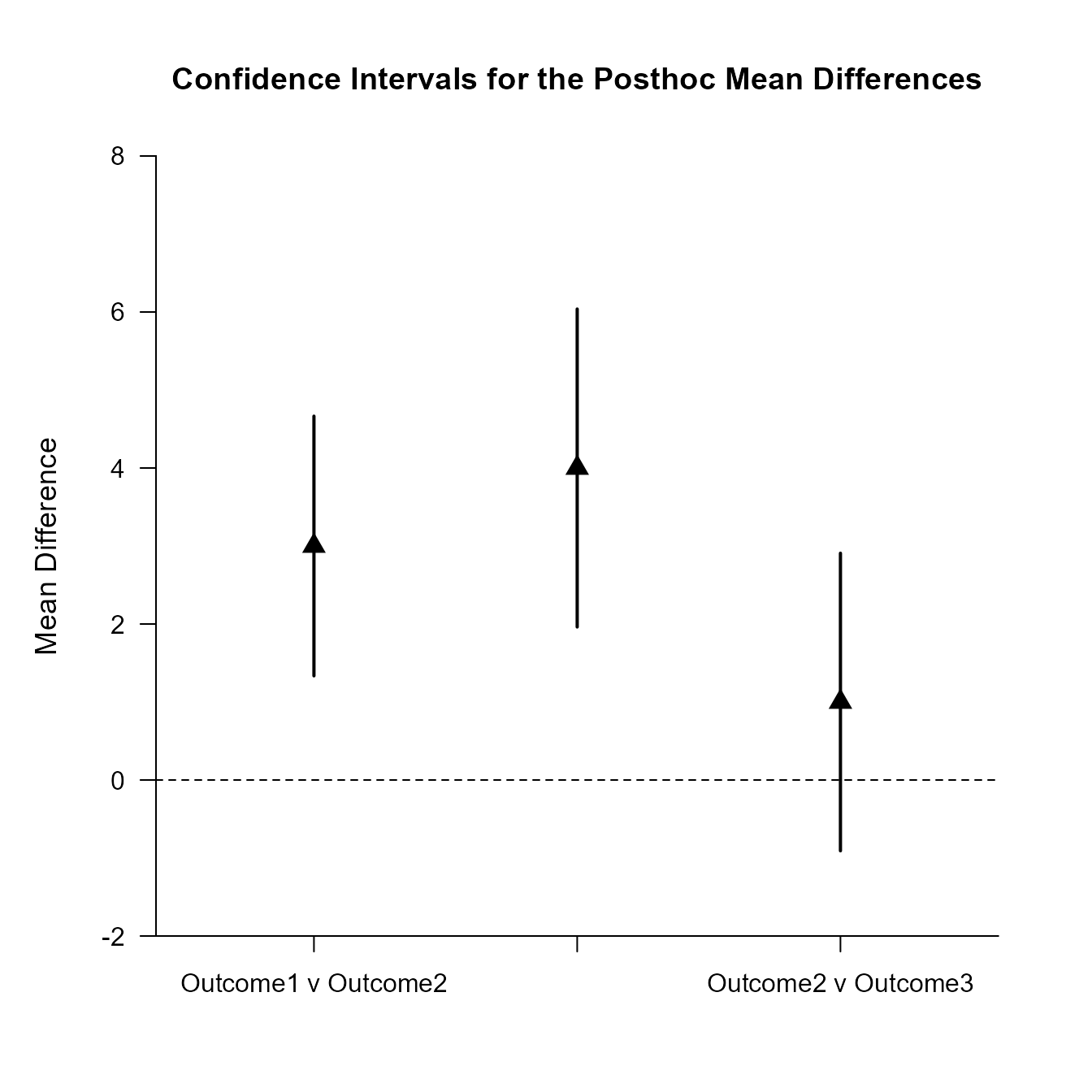
Provide a diffogram (plot of means and the confidence intervals for the post hoc comparisons).
(RepeatedMoments) |> plotPosthocDiffogram(RepeatedCorr)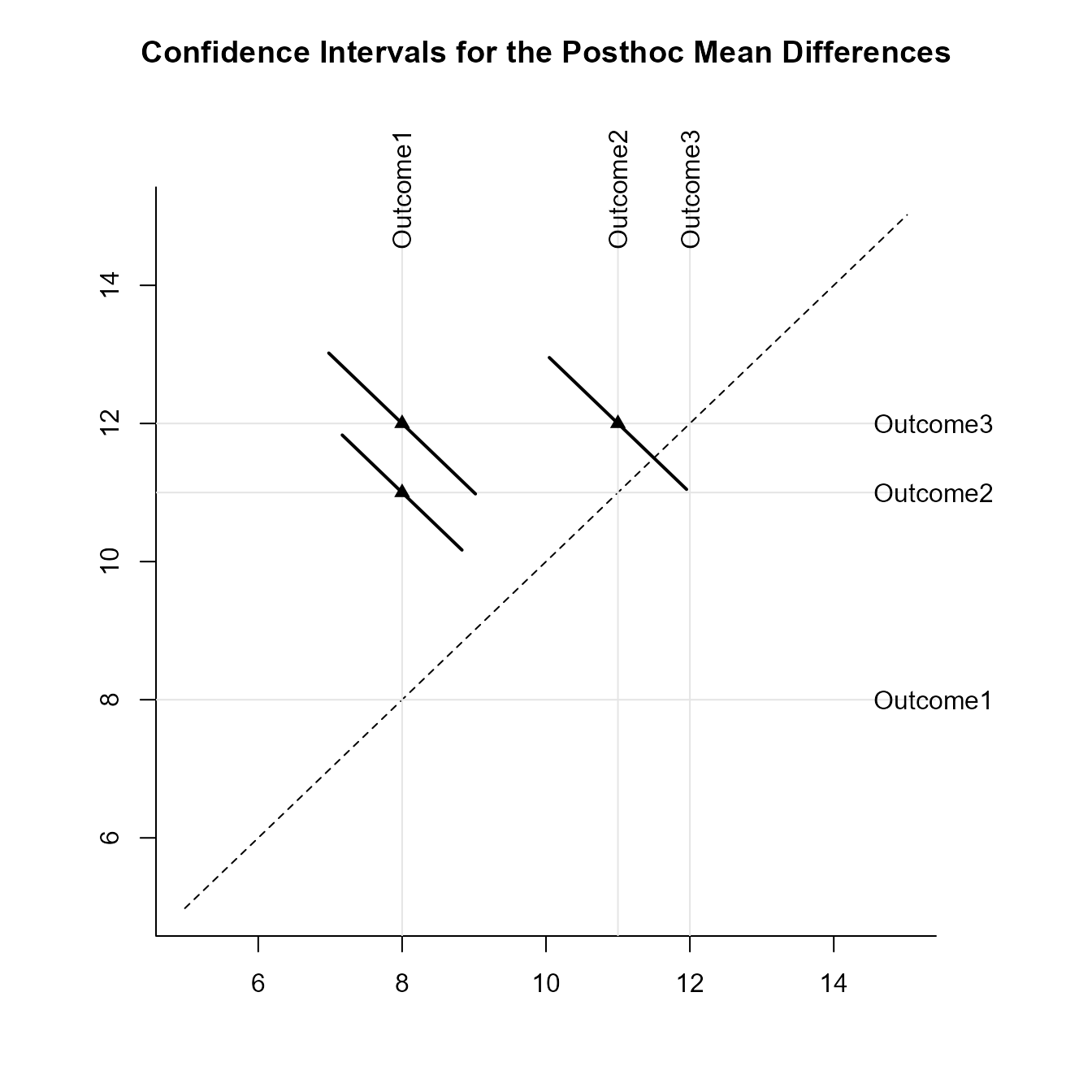
Significance Tests
Test the post hoc comparisons for statistical significance.
(RepeatedMoments) |> testPosthoc(RepeatedCorr)
Hypothesis Tests for the Posthoc Mean Differences
Diff SE df t p
Outcome1 v Outcome2 3.000 0.596 9.000 5.031 0.002
Outcome1 v Outcome3 4.000 0.730 9.000 5.479 0.001
Outcome2 v Outcome3 1.000 0.683 9.000 1.463 0.352Standardized Effect Sizes
Get the standardized effect sizes (and their confidence intervals) for the post hoc comparisons.
(RepeatedMoments) |> standardizePosthoc(RepeatedCorr)
Confidence Intervals for the Posthoc Standardized Mean Differences
d SE LL UL
Outcome1 v Outcome2 1.617 0.466 0.703 2.530
Outcome1 v Outcome3 2.000 0.531 0.959 3.042
Outcome2 v Outcome3 0.429 0.333 -0.224 1.082