OneWay Summary Traditional • EASI

This page examines a single-factor between-subjects (one-way) design using summary statistics input, focusing on omnibus and pairwise analyses.

Preliminary Tasks

Data Entry

This code inputs the group summaries and creates a single summary table.

Level1 <- c(N = 10, M = 8.000, SD = 1.414)
Level2 <- c(N = 10, M = 11.000, SD = 2.211)
Level3 <- c(N = 10, M = 12.000, SD = 2.449)
OneWayMoments <- construct(Level1, Level2, Level3, class = "bsm")

Summary Statistics

This code confirms the descriptive statistics from the summary table.

(OneWayMoments) |> describeMoments()


Summary Statistics for the Data

             N       M      SD
Level1  10.000   8.000   1.414
Level2  10.000  11.000   2.211
Level3  10.000  12.000   2.449

Analyses of the Omnibus Effect

The Analysis of Variance examines the overall differences among the means.

Source Table

Display the source table.

(OneWayMoments) |> describeEffect()


Source Table for the Model

             SS      df      MS
Between  86.667   2.000  43.333
Within  115.970  27.000   4.295

Proportion of Variance Accounted for

Get an estimate of the proportion of variance account for by the factor (and the confidence interval for that estimate).

(OneWayMoments) |> estimateEffect()


Proportion of Variance Accounted For by the Model

           Est      LL      UL
Factor   0.428   0.157   0.569

Significance Test

Test the overall differences for statistical significance.

(OneWayMoments) |> testEffect()


Hypothesis Test for the Model

             F     df1     df2       p
Factor  10.089   2.000  27.000   0.001

Analyses of Pairwise Comparisons

The analyses for the pairwise comparisons do not assume homogeneity of variance and do not make adjustments for multiple comparisons (and are therefore effectively equivalent to a series of independent samples t tests).

Confidence Intervals

Obtain interval estimates for the pairwise comparisons.

(OneWayMoments) |> estimatePairwise()


Confidence Intervals for the Pairwise Mean Differences

                     MD      SE      df      LL      UL
Level1 v Level2   3.000   0.830  15.307   1.234   4.766
Level1 v Level3   4.000   0.894  14.400   2.087   5.913
Level2 v Level3   1.000   1.043  17.815  -1.194   3.194

Provide a traditional plot of the confidence intervals for the pairwise comparisons (including a line that represents no difference for the comparisons).

(OneWayMoments) |> plotPairwise(line = 0, values = FALSE)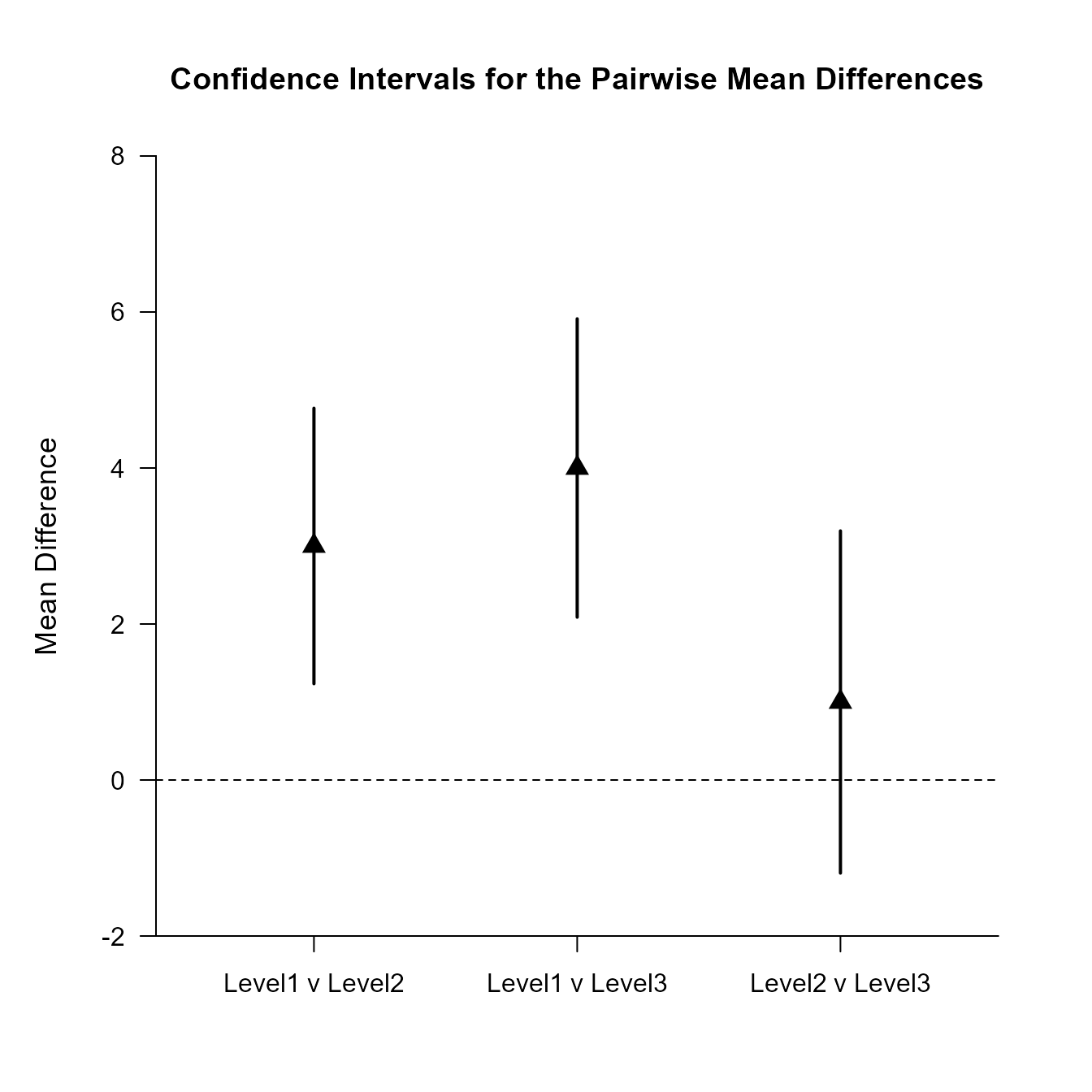

Provide a diffogram (plot of means and the confidence intervals for the pairwise comparisons).

(OneWayMoments) |> plotPairwiseDiffogram()

Significance Tests

Test the pairwise comparisons for statistical significance.

(OneWayMoments) |> testPairwise()


Hypothesis Tests for the Pairwise Mean Differences

                     MD      SE      df       t       p
Level1 v Level2   3.000   0.830  15.307   3.615   0.002
Level1 v Level3   4.000   0.894  14.400   4.473   0.000
Level2 v Level3   1.000   1.043  17.815   0.958   0.351

Standardized Effect Sizes

Get the standardized effect sizes (and their confidence intervals) for the pairwise comparisons.

(OneWayMoments) |> standardizePairwise()


Confidence Intervals for the Pairwise Standardized Mean Differences

                      d      SE      LL      UL
Level1 v Level2   1.617   0.555   0.530   2.704
Level1 v Level3   2.000   0.601   0.823   3.178
Level2 v Level3   0.429   0.477  -0.506   1.363

Analyses of Relational Intervals

Relational intervals are values (and boxes on a graph) that indicate whether two conditions are statistically significantly different. The analyses for the relational confidence intervals do assume homogeneity of variance but do not make adjustments for multiple comparisons.

Provide estimates of the arelational and relational intervals.

(OneWayMoments) |> estimateRelational()


Confidence and Relational Intervals for the Means

             M   RI.LL   RI.UL   CI.LL   CI.UL
Level1   8.000   7.049   8.951   6.988   9.012
Level2  11.000  10.049  11.951   9.418  12.582
Level3  12.000  11.049  12.951  10.248  13.752

Plot the intervals.

(OneWayMoments) |> plotRelational()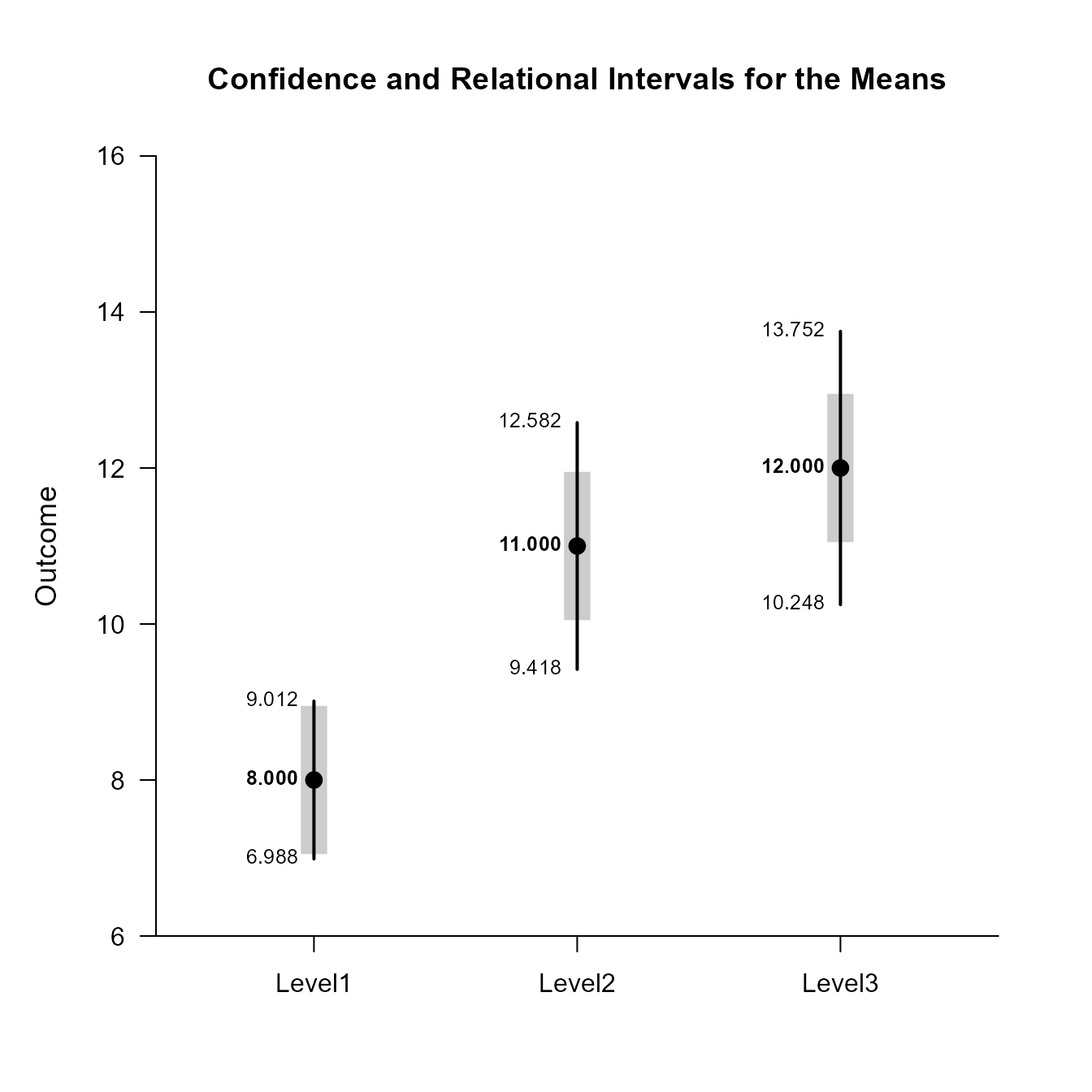

Analyses of Post Hoc Comparisons

The analyses for the post hoc comparisons do assume homogeneity of variance and do make adjustments for multiple comparisons (based on Tukey HSD procedures).

Confidence Intervals

Obtain interval estimates for the post hoc comparisons.

(OneWayMoments) |> estimatePosthoc()


Confidence Intervals for the Posthoc Mean Differences

                   Diff      SE      df      LL      UL
Level1 v Level2   3.000   0.927  27.000   0.702   5.298
Level1 v Level3   4.000   0.927  27.000   1.702   6.298
Level2 v Level3   1.000   0.927  27.000  -1.298   3.298

Provide a traditional plot of the confidence intervals for the post hoc comparisons (including a line that represents no difference for the comparisons).

(OneWayMoments) |> plotPosthoc(line = 0, values = FALSE)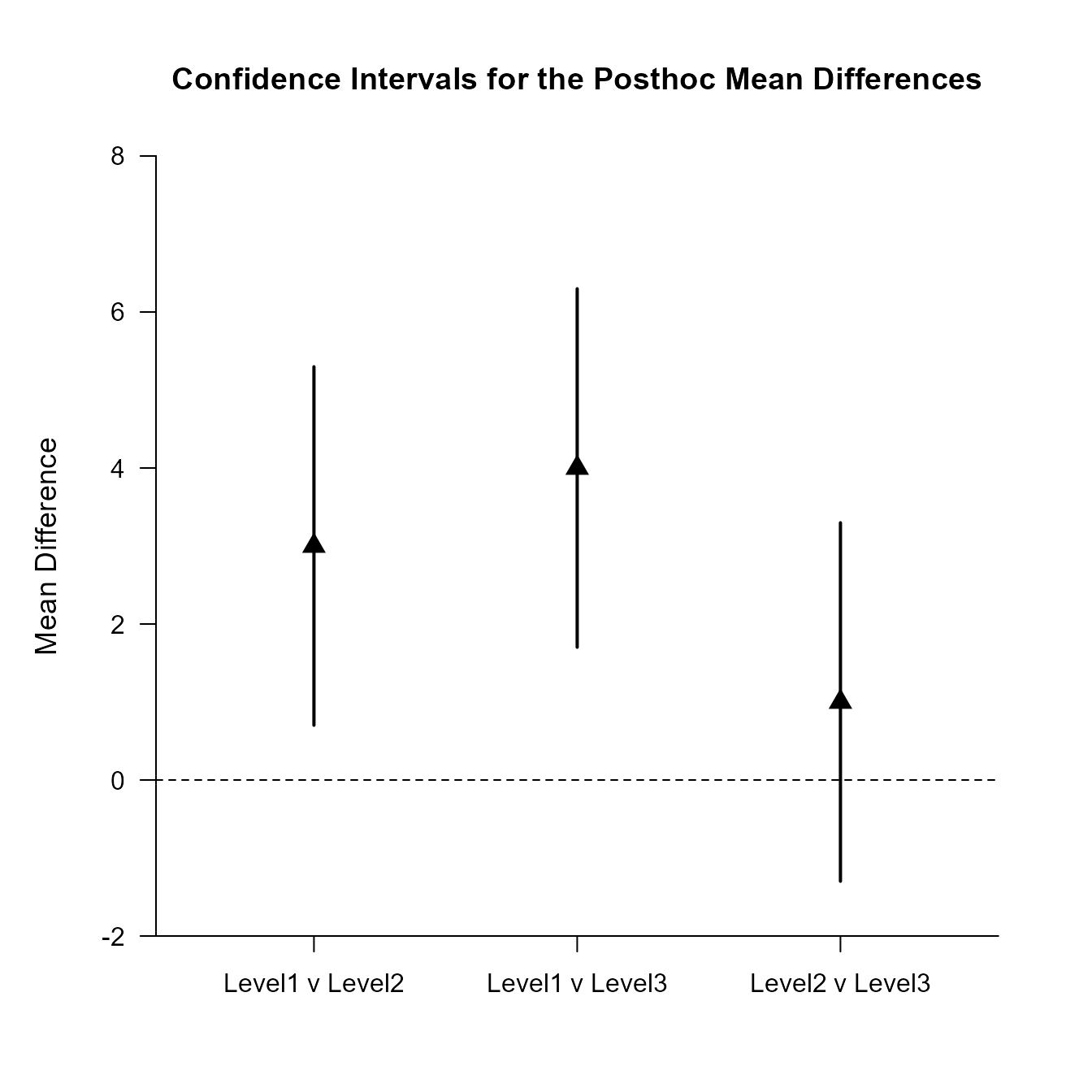

Provide a diffogram (plot of means and the confidence intervals for the post hoc comparisons).

(OneWayMoments) |> plotPosthocDiffogram()

Significance Tests

Test the post hoc comparisons for statistical significance.

(OneWayMoments) |> testPosthoc()


Hypothesis Tests for the Posthoc Mean Differences

                   Diff      SE      df       t       p
Level1 v Level2   3.000   0.927  27.000   3.237   0.009
Level1 v Level3   4.000   0.927  27.000   4.316   0.001
Level2 v Level3   1.000   0.927  27.000   1.079   0.535

Standardized Effect Sizes

Get the standardized effect sizes (and their confidence intervals) for the post hoc comparisons.

(OneWayMoments) |> standardizePosthoc()


Confidence Intervals for the Posthoc Standardized Mean Differences

                      d      SE      LL      UL
Level1 v Level2   1.617   0.555   0.530   2.704
Level1 v Level3   2.000   0.601   0.823   3.178
Level2 v Level3   0.429   0.477  -0.506   1.363