OneWay Summary Contrasts • EASI

This page examines a single-factor between-subjects (one-way) design using summary statistics input, focusing on comparisons and contrasts.

Preliminary Tasks

Data Entry

This code inputs the group summaries and creates a single summary table.

Level1 <- c(N = 10, M = 8.000, SD = 1.414)
Level2 <- c(N = 10, M = 11.000, SD = 2.211)
Level3 <- c(N = 10, M = 12.000, SD = 2.449)
OneWayMoments <- construct(Level1, Level2, Level3, class = "bsm")

Summary Statistics

This code confirms the descriptive statistics from the summary table.

(OneWayMoments) |> describeMoments()


Summary Statistics for the Data

             N       M      SD
Level1  10.000   8.000   1.414
Level2  10.000  11.000   2.211
Level3  10.000  12.000   2.449

Analyses of the Means

This section produces analyses that are equivalent to one-sample analyses separately for each level of a factor.

Confidence Intervals

This code will provide a table of confidence intervals for each level of the factor.

(OneWayMoments) |> estimateMeans()


Confidence Intervals for the Means

           Est      SE      df      LL      UL
Level1   8.000   0.447   9.000   6.988   9.012
Level2  11.000   0.699   9.000   9.418  12.582
Level3  12.000   0.774   9.000  10.248  13.752

This code will produce a graph of the confidence intervals for each level of the factor.

(OneWayMoments) |> plotMeans()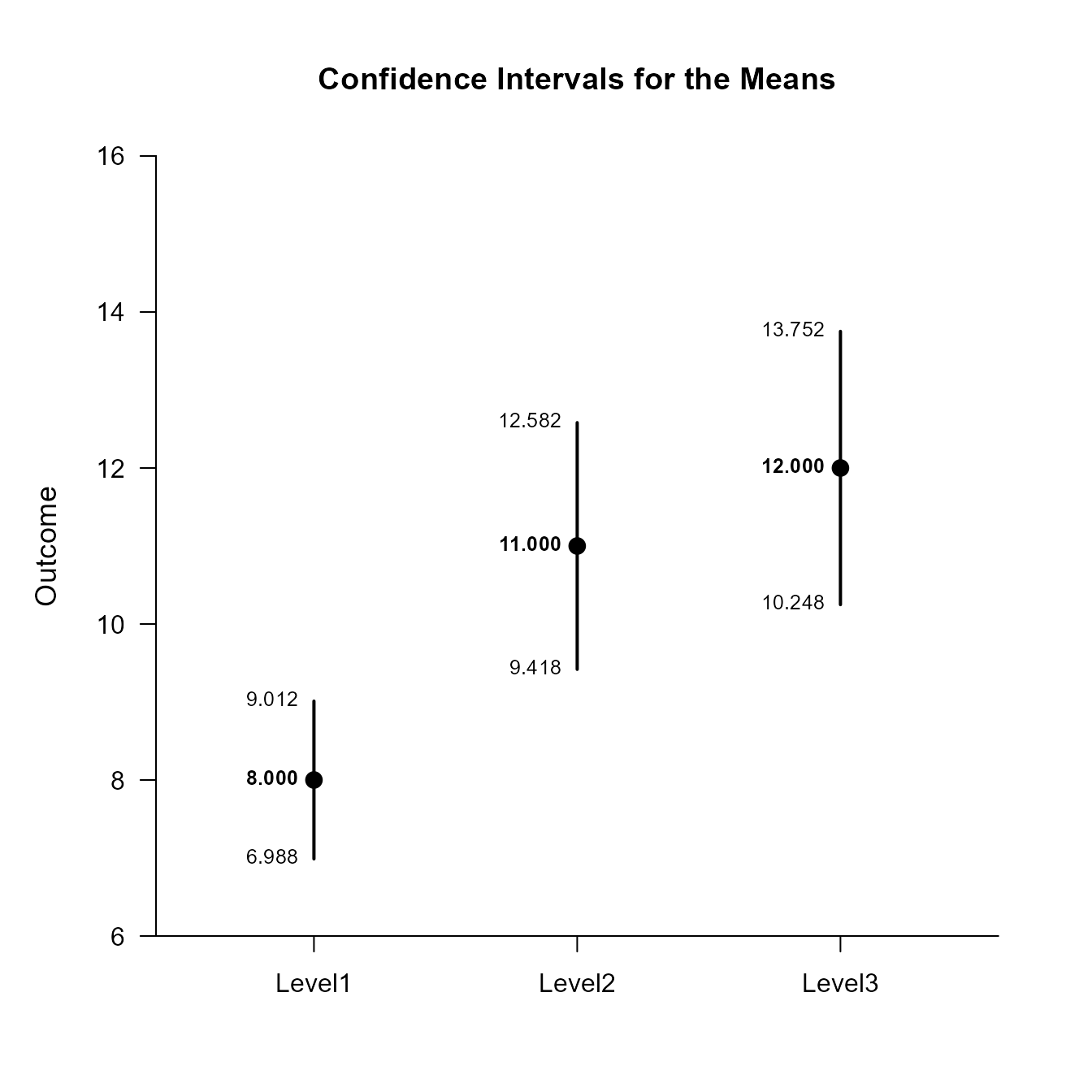

The code defaults to 95% confidence intervals. This can be changed if desired.

(OneWayMoments) |> estimateMeans(conf.level = .99)


Confidence Intervals for the Means

           Est      SE      df      LL      UL
Level1   8.000   0.447   9.000   6.547   9.453
Level2  11.000   0.699   9.000   8.728  13.272
Level3  12.000   0.774   9.000   9.483  14.517

For the graph, it is possible to add a comparison line to represent a population (or test) value and a region of practical equivalence in addition to changing the confidence level.

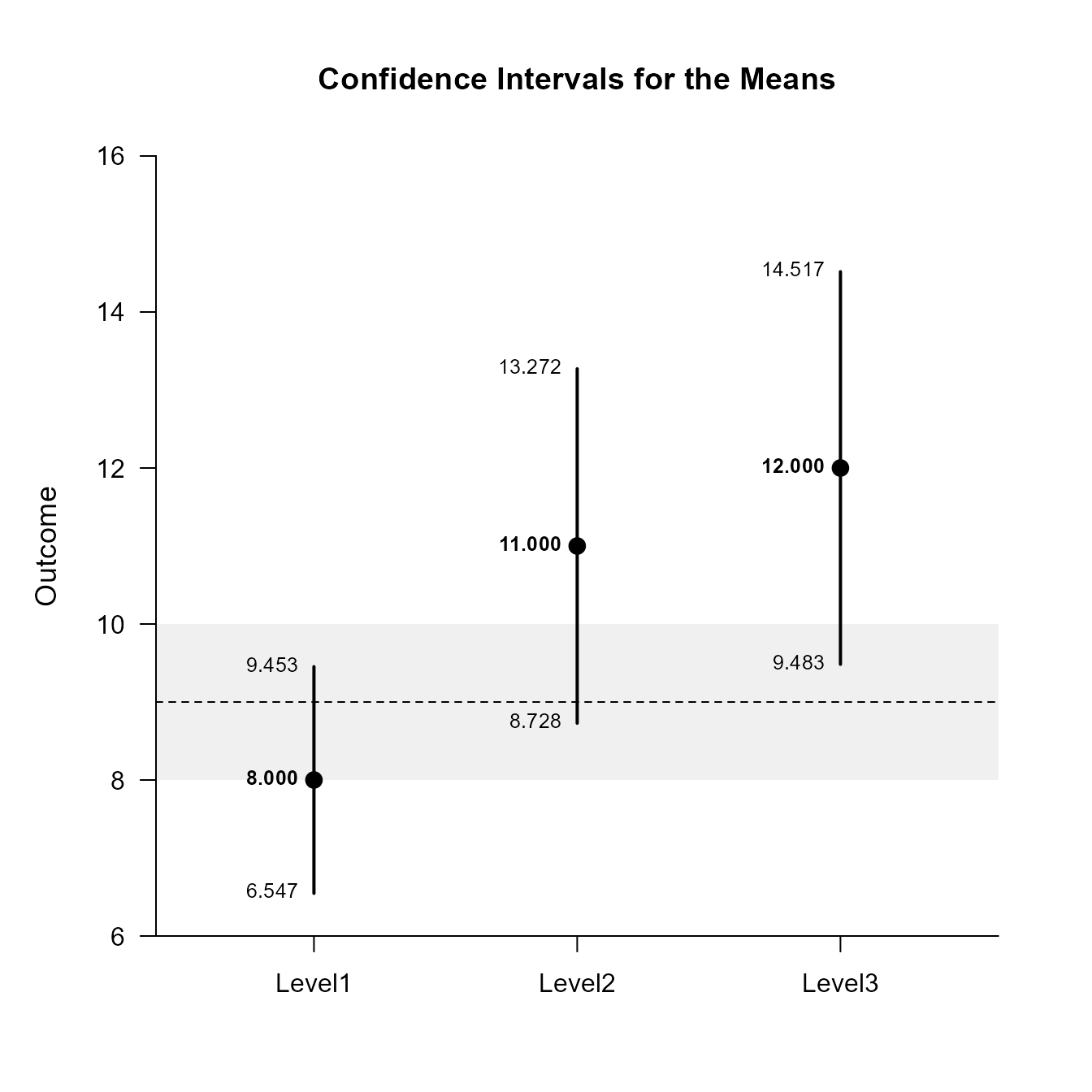
(OneWayMoments) |> plotMeans(conf.level = .99, line = 9, rope = c(8, 10))

Significance Tests

This code will produce a table of NHST separately for each level of the factor. In this case, all the means are tested against a value of zero.

(OneWayMoments) |> testMeans()


Hypothesis Tests for the Means

          Diff      SE      df       t       p
Level1   8.000   0.447   9.000  17.891   0.000
Level2  11.000   0.699   9.000  15.733   0.000
Level3  12.000   0.774   9.000  15.495   0.000

Often, the default test value of zero is not meaningful or plausible. This too can be altered (often in conjunction with what is presented in the plot).

(OneWayMoments) |> testMeans(mu = 9)


Hypothesis Tests for the Means

          Diff      SE      df       t       p
Level1  -1.000   0.447   9.000  -2.236   0.052
Level2   2.000   0.699   9.000   2.860   0.019
Level3   3.000   0.774   9.000   3.874   0.004

Standardized Effect Sizes

This code will produce a table of standardized mean differences separately for each level of the factor. In this case, the mean is compared to zero to form the effect size.

(OneWayMoments) |> standardizeMeans()


Confidence Intervals for the Standardized Means

             d      SE      LL      UL
Level1   5.658   1.251   3.005   8.297
Level2   4.975   1.111   2.622   7.312
Level3   4.900   1.096   2.580   7.204

Here too it is possible to alter the width of the confidence intervals and to establish a more plausible comparison value for the mean.

(OneWayMoments) |> standardizeMeans(mu = 9, conf.level = .99)


Confidence Intervals for the Standardized Means

             d      SE      LL      UL
Level1  -0.707   0.364  -1.614   0.222
Level2   0.905   0.384  -0.083   1.873
Level3   1.225   0.422   0.126   2.317

Analyses of a Comparison

This section produces analyses involving comparisons of two levels of a factor.

Confidence Intervals

This code estimates the confidence interval of the difference.

(OneWayMoments) |> focus("Level1", "Level2") |> estimateDifference()


Confidence Interval for the Mean Difference

               Est      SE      df      LL      UL
Comparison   3.000   0.830  15.307   1.234   4.766

This code obtains and plots the confidence intervals for the mean difference in the identified comparison.

(OneWayMoments) |> focus("Level1", "Level2") |> plotDifference()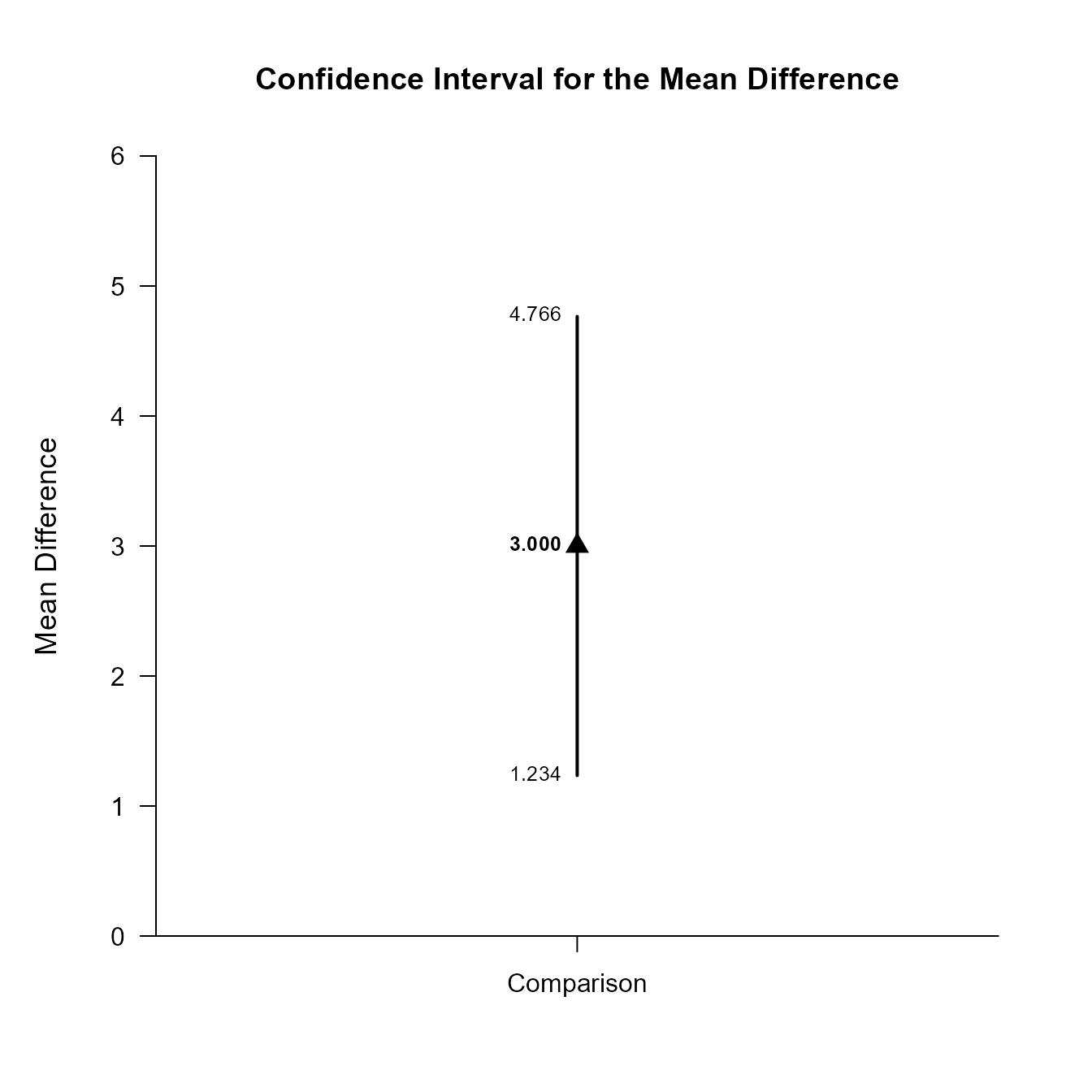

Of course, you can change the confidence level from the default 95% if desired.

(OneWayMoments) |> focus("Level1", "Level2") |> estimateDifference(conf.level = .99)


Confidence Interval for the Mean Difference

               Est      SE      df      LL      UL
Comparison   3.000   0.830  15.307   0.561   5.439

Once again, the confidence levels can be changed away from the default and a comparison line to represent a population (or test) value and a region of practical equivalence can be added to the graph.

(OneWayMoments) |> focus("Level1", "Level2") |> plotDifference(conf.level = .99, line = 0, rope = c(-2, 2))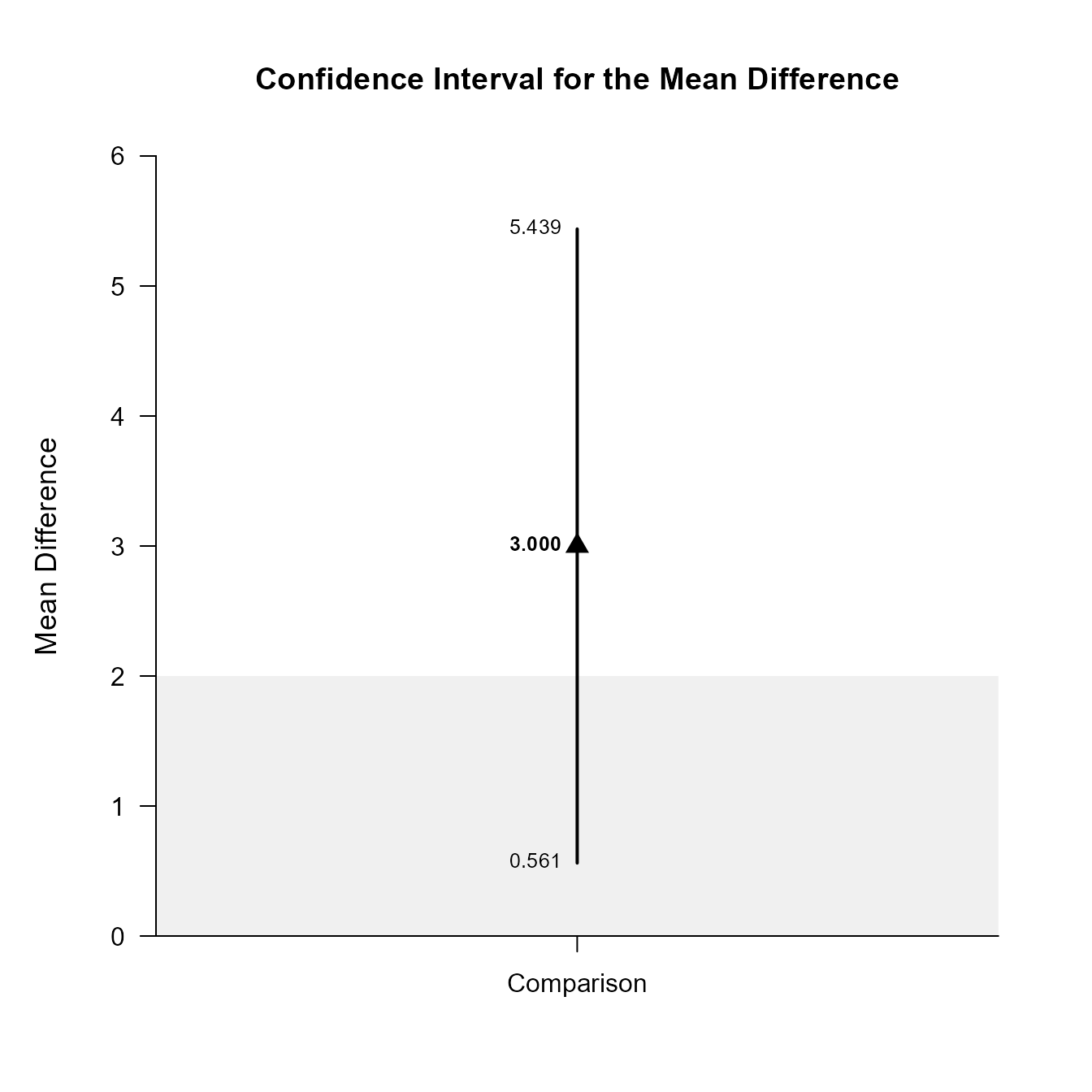

If you wish, you can get the confidence intervals for the means and the mean difference in one command.

(OneWayMoments) |> focus("Level1", "Level2") |> estimateComparison()


Confidence Intervals for the Mean Comparison

               Est      SE      df      LL      UL
Level1       8.000   0.447   9.000   6.988   9.012
Level2      11.000   0.699   9.000   9.418  12.582
Comparison   3.000   0.830  15.307   1.234   4.766

This code produces a difference plot using the confidence intervals for the means and the mean difference.

(OneWayMoments) |> focus("Level1", "Level2") |> plotComparison()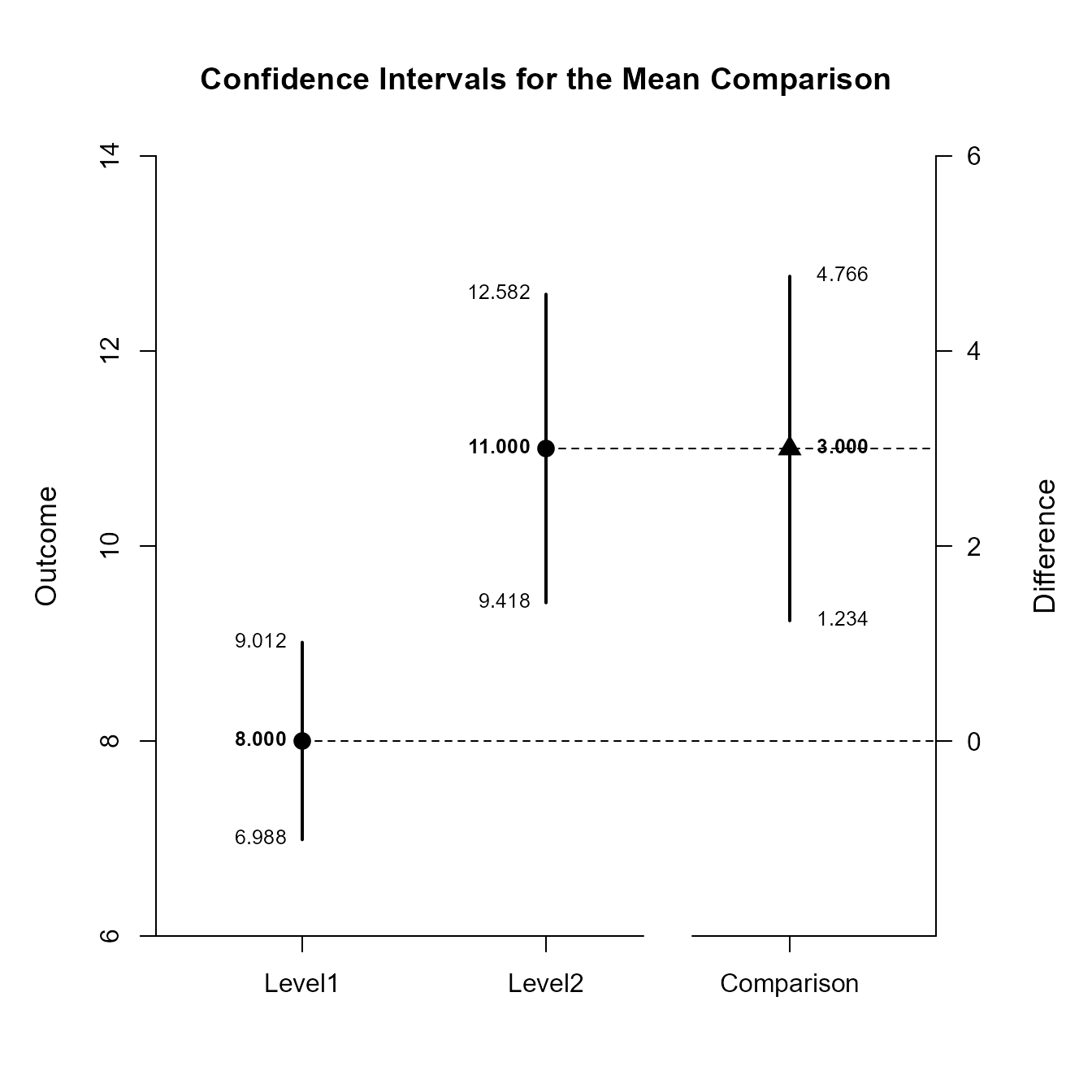

Of course, you can change the confidence level from the default 95% if desired.

(OneWayMoments) |> focus("Level1", "Level2") |> estimateComparison(conf.level = .99)


Confidence Intervals for the Mean Comparison

               Est      SE      df      LL      UL
Level1       8.000   0.447   9.000   6.547   9.453
Level2      11.000   0.699   9.000   8.728  13.272
Comparison   3.000   0.830  15.307   0.561   5.439

Once again, the confidence levels can be changed away from the default and a region of practical equivalence can be added to the graph.

(OneWayMoments) |> focus("Level1", "Level2") |> plotComparison(conf.level = .99, rope = c(-2, 2))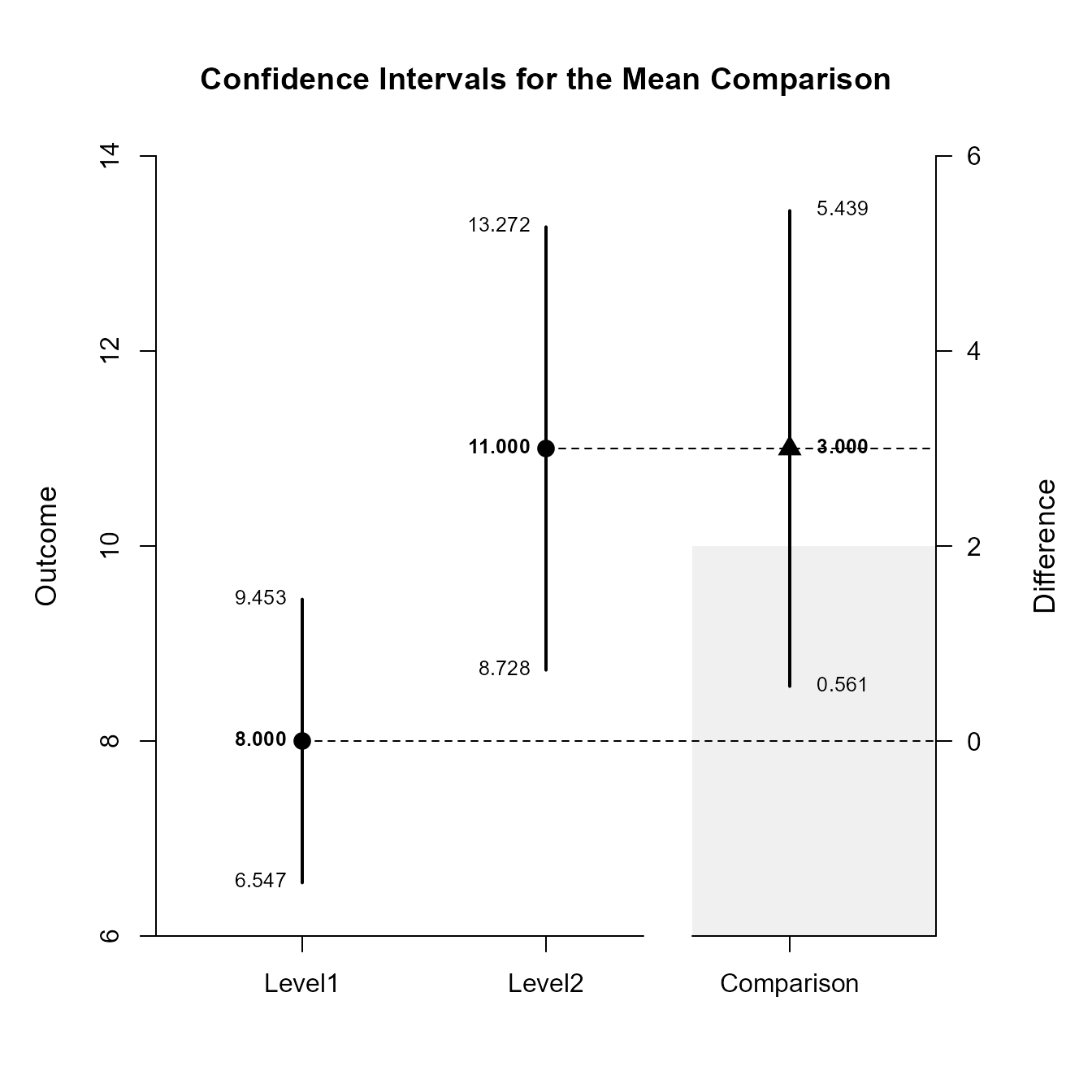

Significance Test

This code produces NHST for the identified comparison (using a default test value of zero).

(OneWayMoments) |> focus("Level1", "Level2") |> testDifference()


Hypothesis Test for the Mean Difference

              Diff      SE      df       t       p
Comparison   3.000   0.830  15.307   3.615   0.002

If the default value of zero is not plausible, it too can be changed.

(OneWayMoments) |> focus("Level1", "Level2") |> testDifference(mu = -2)


Hypothesis Test for the Mean Difference

              Diff      SE      df       t       p
Comparison   5.000   0.830  15.307   6.025   0.000

Standardized Effect Size

This code calculates a standardized mean difference for the comparison and its confidence interval.

(OneWayMoments) |> focus("Level1", "Level2") |> standardizeDifference()


Confidence Interval for the Standardized Mean Difference

                 d      SE      LL      UL
Comparison   1.617   0.555   0.530   2.704

The width of the confidence interval for the effect size can be altered if desired.

(OneWayMoments) |> focus("Level1", "Level2") |> standardizeDifference(conf.level = .99)


Confidence Interval for the Standardized Mean Difference

                 d      SE      LL      UL
Comparison   1.617   0.555   0.188   3.045

Analyses of a Contrast

This section produces analyses involving multiple levels of a factor.

Confidence Intervals

This code produces a confidence interval for a specified contrast.

(OneWayMoments) |> estimateContrast(contrast = c(-1, .5, .5))


Confidence Interval for the Mean Contrast

             Est      SE      df      LL      UL
Contrast   3.500   0.687  25.917   2.087   4.913

This code obtains and plots the confidence intervals for the groups and the mean difference in the identified contrast.

(OneWayMoments) |> plotContrast(contrast = c(-1, .5, .5))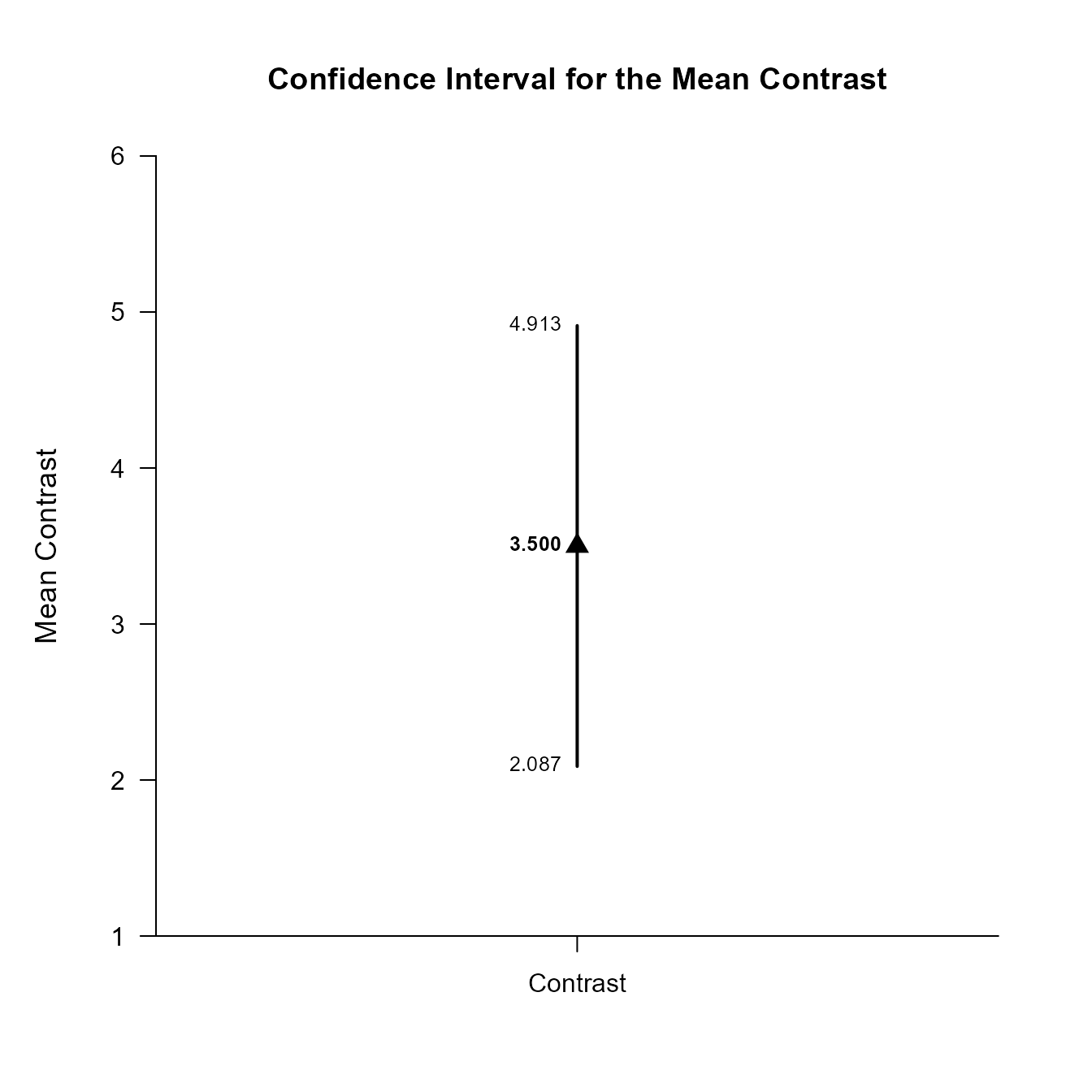

As in all other cases, the default value of the confidence interval can be changed.

(OneWayMoments) |> estimateContrast(contrast = c(-1, .5, .5), conf.level = .99)


Confidence Interval for the Mean Contrast

             Est      SE      df      LL      UL
Contrast   3.500   0.687  25.917   1.590   5.410

The width of the confidence interval for the contrast can be altered and a comparison line to represent a population (or test) value and a region of practical equivalence can be added to the graph.

(OneWayMoments) |> plotContrast(contrast = c(-1, .5, .5), conf.level = .99, line = 0, rope = c(-2, 2))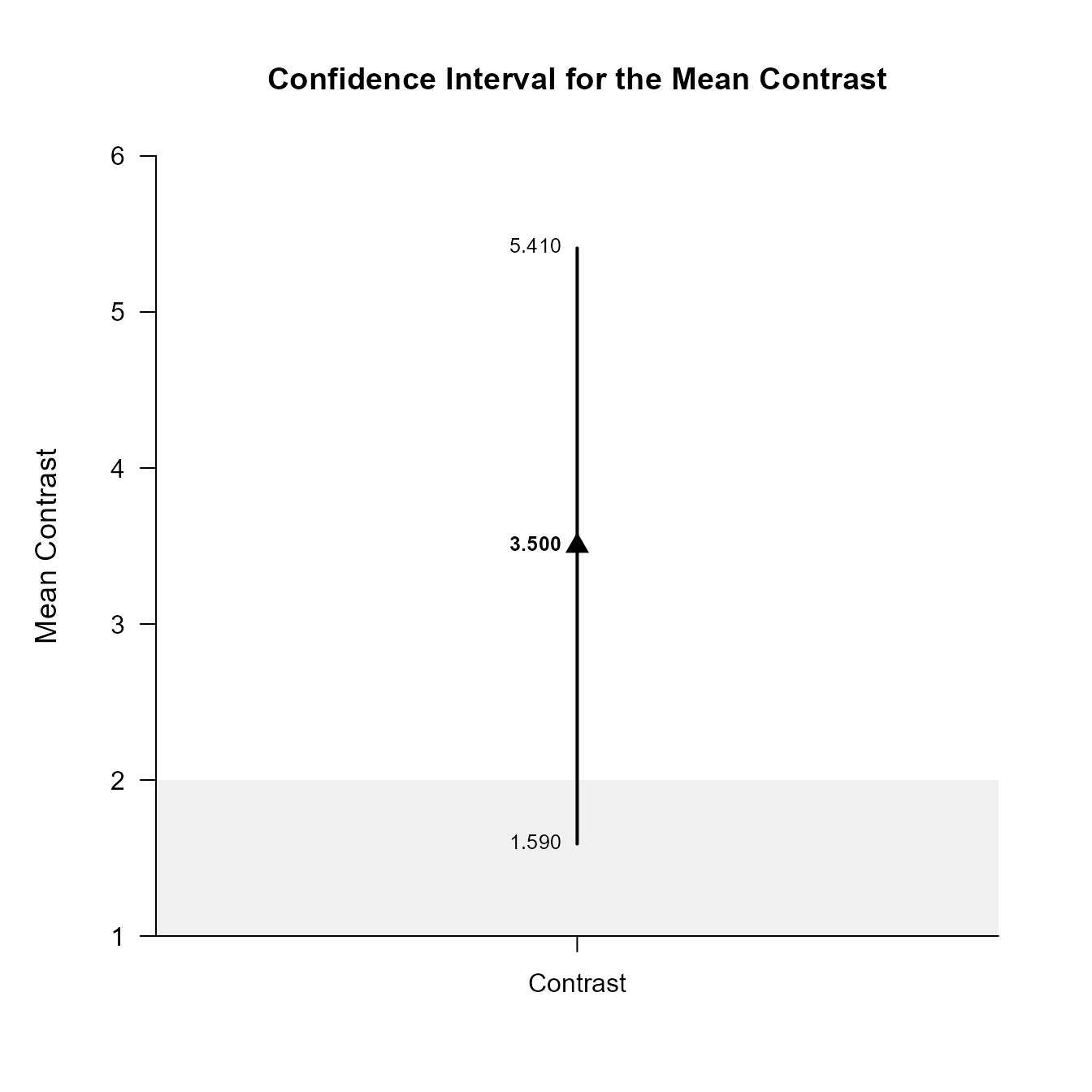

If you wish, you can get the confidence intervals for the mean subsets and the mean contrast in one command.

(OneWayMoments) |> estimateSubsets(contrast = c(-1, .5, .5))


Confidence Intervals for the Mean Subsets

                 Est      SE      df      LL      UL
Neg Weighted   8.000   0.447   9.000   6.988   9.012
Pos Weighted  11.500   0.522  17.815  10.403  12.597
Contrast       3.500   0.687  25.917   2.087   4.913

This code produces a difference plot using the confidence intervals for the mean subsets and the mean contrast.

(OneWayMoments) |> plotSubsets(contrast = c(-1, .5, .5))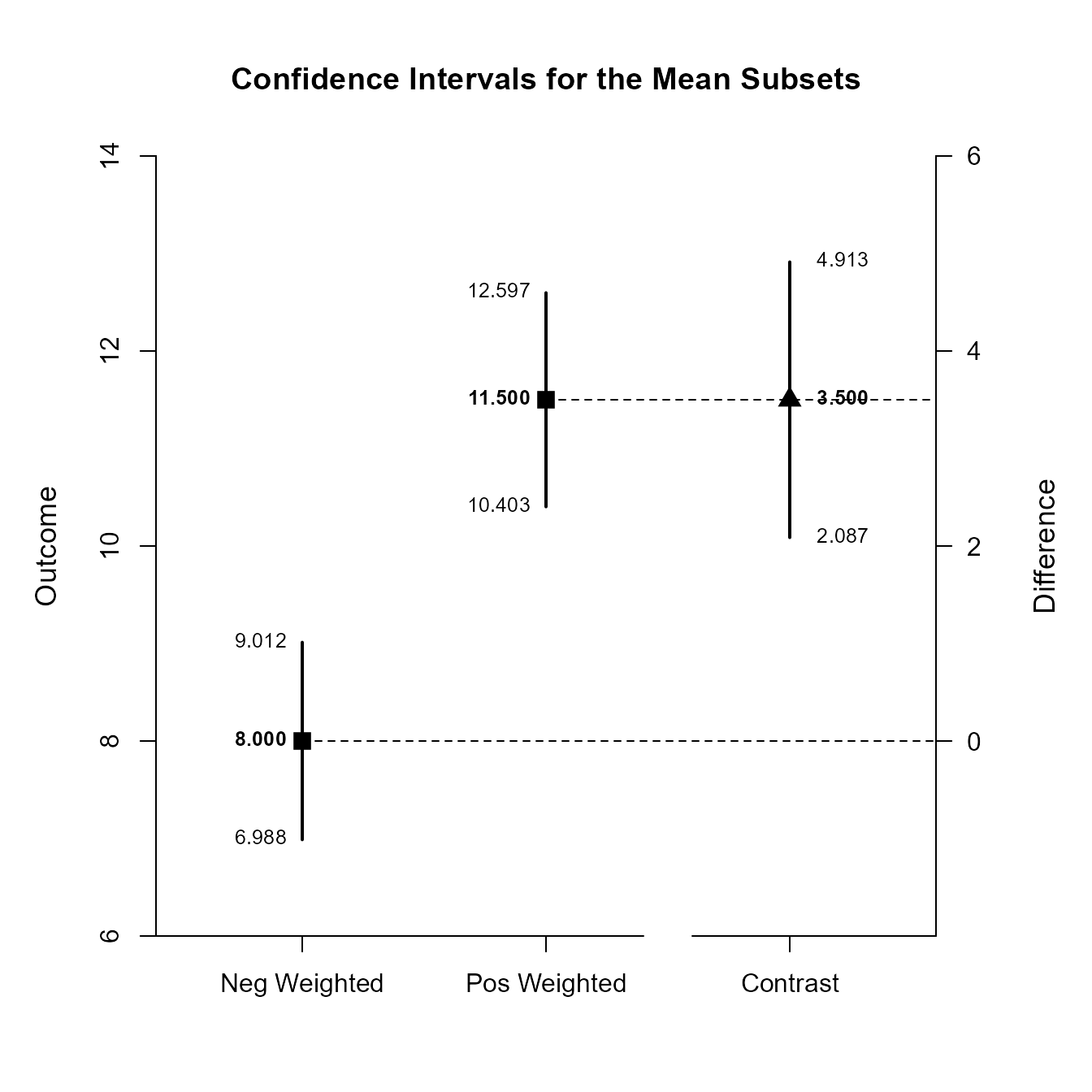

Of course, you can change the confidence level from the default 95% if desired.

(OneWayMoments) |> estimateSubsets(contrast = c(-1, .5, .5), conf.level = .99)


Confidence Intervals for the Mean Subsets

                 Est      SE      df      LL      UL
Neg Weighted   8.000   0.447   9.000   6.547   9.453
Pos Weighted  11.500   0.522  17.815   9.997  13.003
Contrast       3.500   0.687  25.917   1.590   5.410

Once again, the confidence levels can be changed away from the default and a region of practical equivalence can be added to the graph.

(OneWayMoments) |> plotSubsets(contrast = c(-1, .5, .5), labels = c("Level1", "Others"), conf.level = .99, rope = c(-2, 2))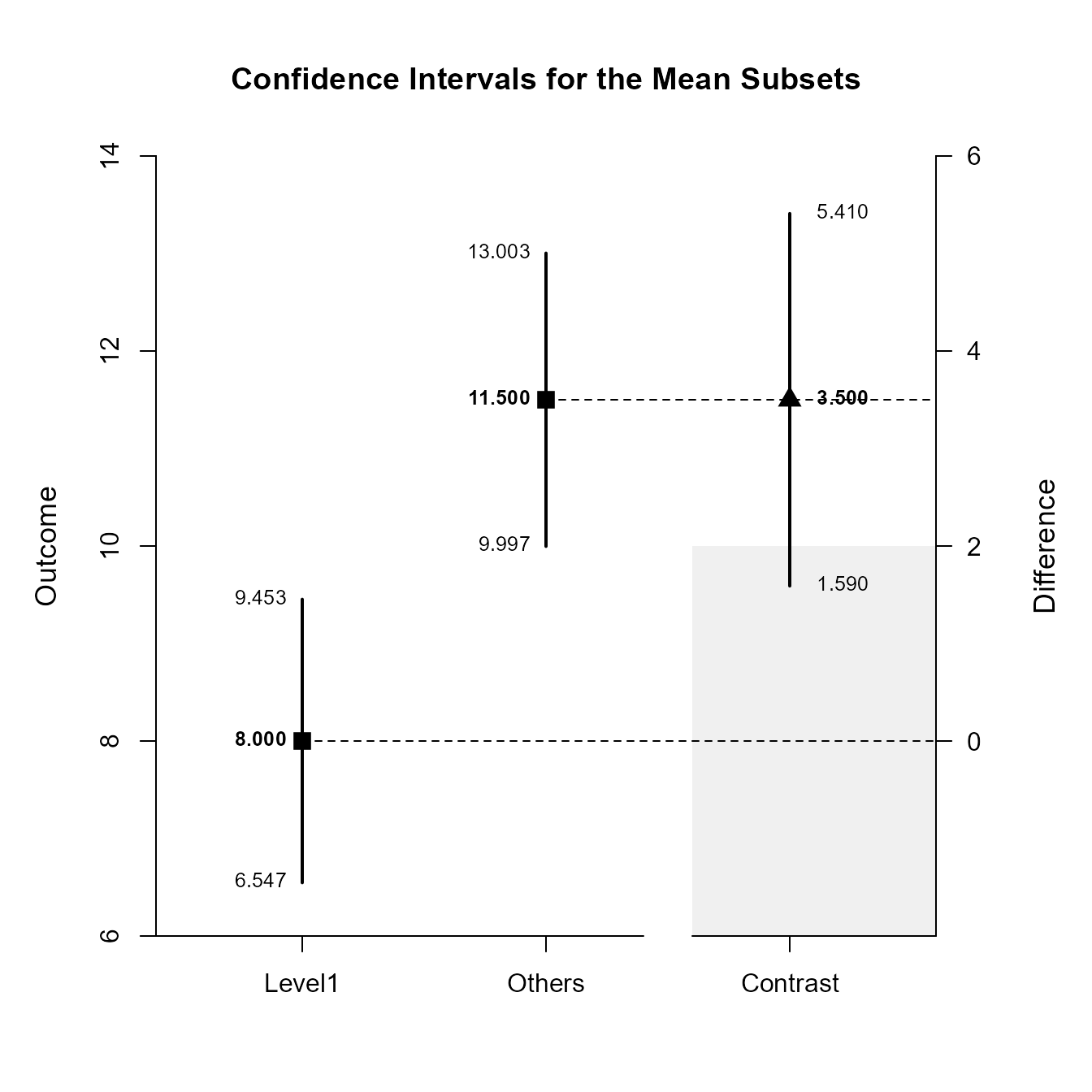

Significance Test

This code produces a NHST for the identified contrast. It tests the contrast against a value of zero by default.

(OneWayMoments) |> testContrast(contrast = c(-1, .5, .5))


Hypothesis Test for the Mean Contrast

             Est      SE      df       t       p
Contrast   3.500   0.687  25.917   5.094   0.000

If desired, the contrast can be tested against other values.

(OneWayMoments) |> testContrast(contrast = c(-1, .5, .5), mu = 4)


Hypothesis Test for the Mean Contrast

             Est      SE      df       t       p
Contrast  -0.500   0.687  25.917  -0.728   0.473

Standardized Effect Size

This code calculates a standardized contrast and its confidence interval.

(OneWayMoments) |> standardizeContrast(contrast = c(-1, .5, .5))


Confidence Interval for the Standardized Mean Contrast

             Est      SE      LL      UL
Contrast   1.689   0.428   0.850   2.527

The width of the confidence interval for the effect size can be altered if desired.

(OneWayMoments) |> standardizeContrast(contrast = c(-1, .5, .5), conf.level = .99)


Confidence Interval for the Standardized Mean Contrast

             Est      SE      LL      UL
Contrast   1.689   0.428   0.587   2.791

Analyses of a Complex Contrast

This section examines a complex contrast among multiple means.

Confidence Intervals

Create a single contrast to compare the first group to the grand mean (which requires some arithmetic). Then estimate and plot the contrast.

(OneWayMoments) |> estimateContrast(contrast = c(2/3, -1/3, -1/3))


Confidence Interval for the Mean Contrast

             Est      SE      df      LL      UL
Contrast  -2.333   0.458  25.917  -3.275  -1.392

(OneWayMoments) |> plotContrast(contrast = c(2/3, -1/3, -1/3))

Rather than setting just one contrast, set two contrasts: one for the Grand Mean and one for Level 1. Estimate and plot the confidence intervals for each contrast and the difference between contrasts.

(OneWayMoments) |> estimateComplex(contrast1 = c(1/3, 1/3, 1/3), contrast2 = c(1, 0, 0), labels = c("GrandMean", "L1Only"))


Confidence Intervals for the Mean Contrasts

              Est      SE      df      LL      UL
GrandMean  10.333   0.378  23.398   9.551  11.115
L1Only      8.000   0.447   9.000   6.988   9.012
Contrast   -2.333   0.458  25.917  -3.275  -1.392

(OneWayMoments) |> plotComplex(contrast1 = c(1/3, 1/3, 1/3), contrast2 = c(1, 0, 0), labels = c("GrandMean", "L1Only"))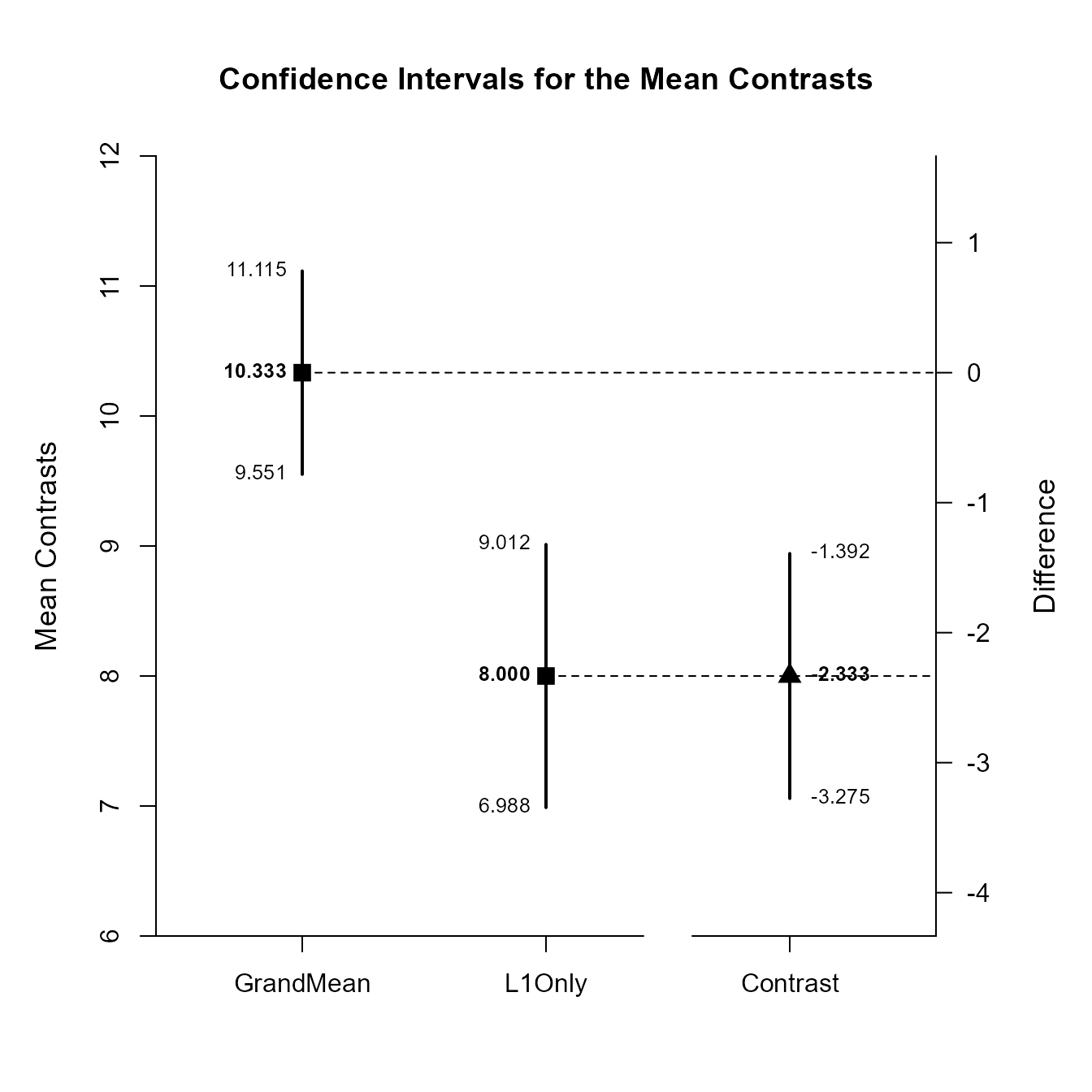

Significance Tests

The two versions of the contrast can be tested for statistical significance.

(OneWayMoments) |> testContrast(contrast = c(2/3, -1/3, -1/3))


Hypothesis Test for the Mean Contrast

             Est      SE      df       t       p
Contrast  -2.333   0.458  25.917  -5.094   0.000

(OneWayMoments) |> testComplex(contrast1 = c(1/3, 1/3, 1/3), contrast2 = c(1, 0, 0), labels = c("GrandMean", "L1Only"))


Hypothesis Tests for the Mean Contrasts

              Est      SE      df       t       p
GrandMean  10.333   0.378  23.398  27.309   0.000
L1Only      8.000   0.447   9.000  17.891   0.000
Contrast   -2.333   0.458  25.917  -5.094   0.000