This page examines a two-factor mixed design (one between-subjects and one within-subjects factor) using summary statistics input, focusing on comparisons and contrasts.
Preliminary Tasks
Data Entry
This code inputs the variable summaries and creates a summary table.
Outcome1 <- c(N = 10, M = 8.000, SD = 1.414)
Outcome2 <- c(N = 10, M = 11.000, SD = 2.211)
Outcome3 <- c(N = 10, M = 12.000, SD = 2.449)
MixedMomentsL1 <- construct(Outcome1, Outcome2, Outcome3, class = "wsm")
Outcome1 <- c(N = 10, M = 8.000, SD = 2.449)
Outcome2 <- c(N = 10, M = 8.000, SD = 2.000)
Outcome3 <- c(N = 10, M = 7.000, SD = 2.211)
MixedMomentsL2 <- construct(Outcome1, Outcome2, Outcome3, class = "wsm")
MixedMoments <- combine(L1 = MixedMomentsL1, L2 = MixedMomentsL2)This code creates correlation matrices.
Outcome1 <- c(1.000, .533, .385)
Outcome2 <- c(.533, 1.000, .574)
Outcome3 <- c(.385, .574, 1.000)
MixedCorrsL1 <- construct(Outcome1, Outcome2, Outcome3, class = "cor")
Outcome1 <- c(1.000, .408, .164)
Outcome2 <- c(.408, 1.000, .553)
Outcome3 <- c(.164, .553, 1.000)
MixedCorrsL2 <- construct(Outcome1, Outcome2, Outcome3, class = "cor")
MixedCorrs <- combine(L1 = MixedCorrsL1, L2 = MixedCorrsL2)Summary Statistics
This code obtains the descriptive statistics as separate tables, each corresponding to a simple effect.
(MixedMomentsL1) |> describeMoments()
Summary Statistics for the Data
N M SD
Outcome1 10.000 8.000 1.414
Outcome2 10.000 11.000 2.211
Outcome3 10.000 12.000 2.449
(MixedCorrsL1) |> describeCorrelations()
Correlations for the Data
Outcome1 Outcome2 Outcome3
Outcome1 1.000 0.533 0.385
Outcome2 0.533 1.000 0.574
Outcome3 0.385 0.574 1.000
(MixedMomentsL2) |> describeMoments()
Summary Statistics for the Data
N M SD
Outcome1 10.000 8.000 2.449
Outcome2 10.000 8.000 2.000
Outcome3 10.000 7.000 2.211
(MixedCorrsL2) |> describeCorrelations()
Correlations for the Data
Outcome1 Outcome2 Outcome3
Outcome1 1.000 0.408 0.164
Outcome2 0.408 1.000 0.553
Outcome3 0.164 0.553 1.000 These statistics can also be confirmed using fewer function calls, a procedure that is then paralleled for the subsequent analyses.
(MixedMoments) |> describeMoments()$L1
Summary Statistics for the Data
N M SD
Outcome1 10.000 8.000 1.414
Outcome2 10.000 11.000 2.211
Outcome3 10.000 12.000 2.449
$L2
Summary Statistics for the Data
N M SD
Outcome1 10.000 8.000 2.449
Outcome2 10.000 8.000 2.000
Outcome3 10.000 7.000 2.211
(MixedCorrs) |> describeCorrelations()$L1
Correlations for the Data
Outcome1 Outcome2 Outcome3
Outcome1 1.000 0.533 0.385
Outcome2 0.533 1.000 0.574
Outcome3 0.385 0.574 1.000
$L2
Correlations for the Data
Outcome1 Outcome2 Outcome3
Outcome1 1.000 0.408 0.164
Outcome2 0.408 1.000 0.553
Outcome3 0.164 0.553 1.000 Analyses of the Means
This section produces analyses that are equivalent to one-sample analyses separately for each level of a factor.
Confidence Intervals
This code will provide tables of confidence intervals for each level of the factor.
(MixedMoments) |> estimateMeans()$L1
Confidence Intervals for the Means
Est SE df LL UL
Outcome1 8.000 0.447 9.000 6.988 9.012
Outcome2 11.000 0.699 9.000 9.418 12.582
Outcome3 12.000 0.774 9.000 10.248 13.752
$L2
Confidence Intervals for the Means
Est SE df LL UL
Outcome1 8.000 0.774 9.000 6.248 9.752
Outcome2 8.000 0.632 9.000 6.569 9.431
Outcome3 7.000 0.699 9.000 5.418 8.582This code will produce a graph of the confidence intervals for each level of the factor.
(MixedMoments) |> plotMeans()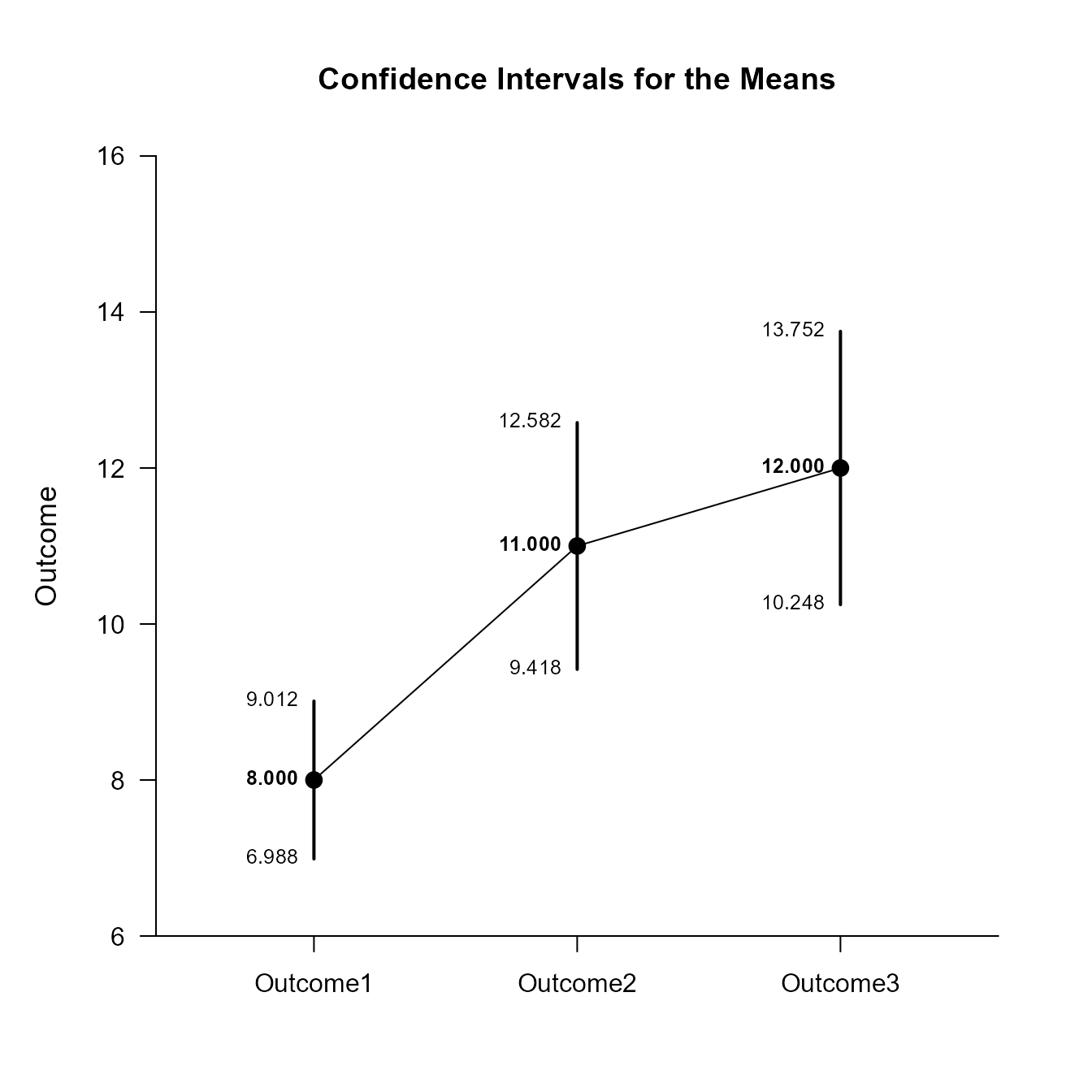
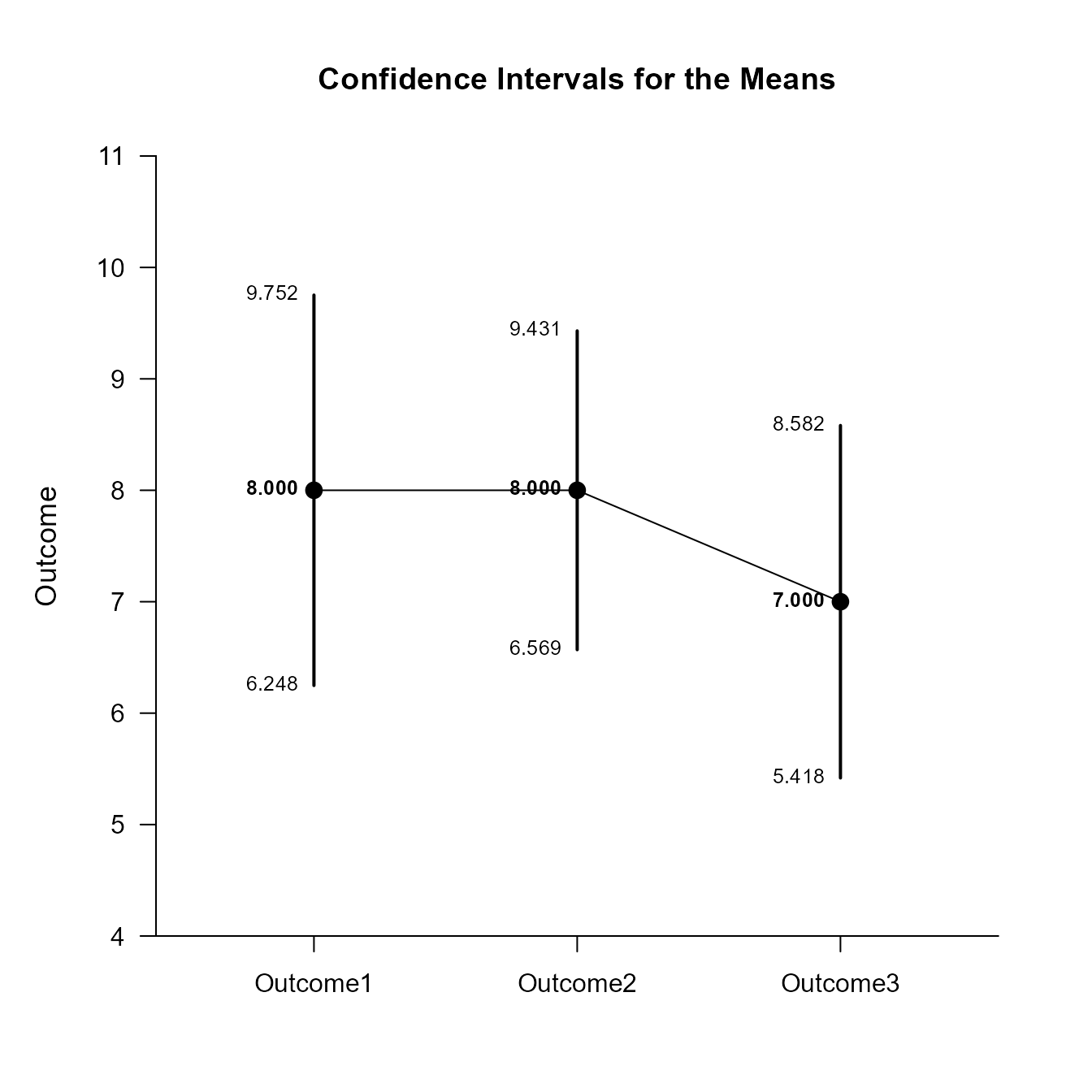
The code defaults to 95% confidence intervals. This can be changed if desired.
(MixedMoments) |> estimateMeans(conf.level = .99)$L1
Confidence Intervals for the Means
Est SE df LL UL
Outcome1 8.000 0.447 9.000 6.547 9.453
Outcome2 11.000 0.699 9.000 8.728 13.272
Outcome3 12.000 0.774 9.000 9.483 14.517
$L2
Confidence Intervals for the Means
Est SE df LL UL
Outcome1 8.000 0.774 9.000 5.483 10.517
Outcome2 8.000 0.632 9.000 5.945 10.055
Outcome3 7.000 0.699 9.000 4.728 9.272For the graph, it is possible to add a comparison line to represent a population (or test) value and a region of practical equivalence in addition to changing the confidence level.
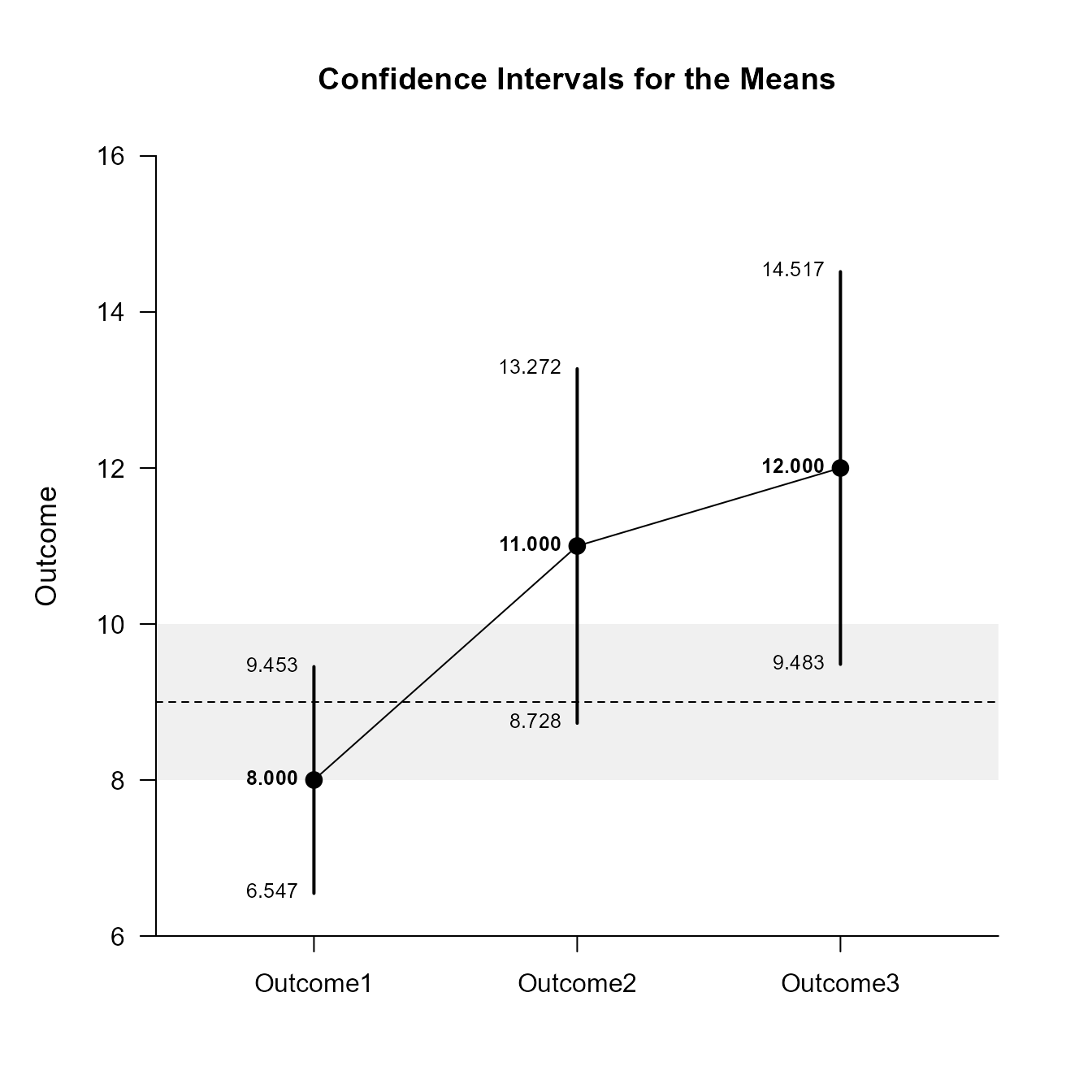
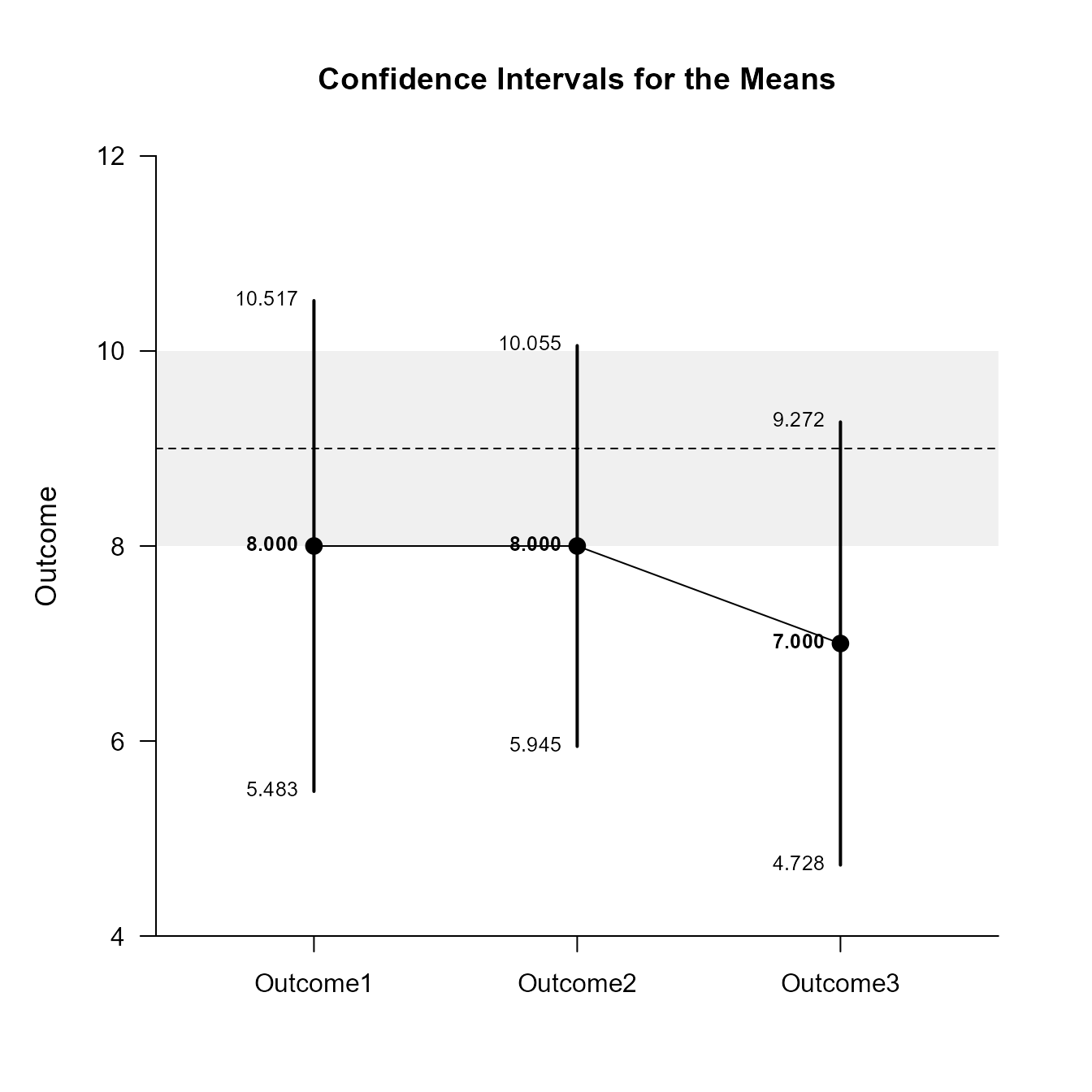
Significance Tests
This code will produce a table of NHST separately for each level of the factor. In this case, all the means are tested against a value of zero.
(MixedMoments) |> testMeans()$L1
Hypothesis Tests for the Means
Diff SE df t p
Outcome1 8.000 0.447 9.000 17.891 0.000
Outcome2 11.000 0.699 9.000 15.733 0.000
Outcome3 12.000 0.774 9.000 15.495 0.000
$L2
Hypothesis Tests for the Means
Diff SE df t p
Outcome1 8.000 0.774 9.000 10.330 0.000
Outcome2 8.000 0.632 9.000 12.649 0.000
Outcome3 7.000 0.699 9.000 10.012 0.000Often, the default test value of zero is not meaningful or plausible. This too can be altered (often in conjunction with what is presented in the plot).
(MixedMoments) |> testMeans(mu = 9)$L1
Hypothesis Tests for the Means
Diff SE df t p
Outcome1 -1.000 0.447 9.000 -2.236 0.052
Outcome2 2.000 0.699 9.000 2.860 0.019
Outcome3 3.000 0.774 9.000 3.874 0.004
$L2
Hypothesis Tests for the Means
Diff SE df t p
Outcome1 -1.000 0.774 9.000 -1.291 0.229
Outcome2 -1.000 0.632 9.000 -1.581 0.148
Outcome3 -2.000 0.699 9.000 -2.860 0.019Standardized Effect Sizes
This code will produce a table of standardized mean differences separately for each level of the factor. In this case, the mean is compared to zero to form the effect size.
(MixedMoments) |> standardizeMeans()$L1
Confidence Intervals for the Standardized Means
d SE LL UL
Outcome1 5.658 1.251 3.005 8.297
Outcome2 4.975 1.111 2.622 7.312
Outcome3 4.900 1.096 2.580 7.204
$L2
Confidence Intervals for the Standardized Means
d SE LL UL
Outcome1 3.267 0.771 1.645 4.864
Outcome2 4.000 0.915 2.068 5.911
Outcome3 3.166 0.752 1.586 4.721Here too it is possible to alter the width of the confidence intervals and to establish a more plausible comparison value for the mean.
(MixedMoments) |> standardizeMeans(mu = 9, conf.level = .99)$L1
Confidence Intervals for the Standardized Means
d SE LL UL
Outcome1 -0.707 0.364 -1.614 0.222
Outcome2 0.905 0.384 -0.083 1.873
Outcome3 1.225 0.422 0.126 2.317
$L2
Confidence Intervals for the Standardized Means
d SE LL UL
Outcome1 -0.408 0.343 -1.249 0.451
Outcome2 -0.500 0.348 -1.357 0.378
Outcome3 -0.905 0.384 -1.873 0.083Analyses of a Comparison
This section produces analyses involving comparisons of two levels of a factor.
Confidence Intervals
This code identifies the two levels for comparison and estimates the confidence interval of the difference.
(MixedMoments) |> focus(Outcome1, Outcome2) |> estimateDifference(MixedCorrs)$L1
Confidence Interval for the Mean Difference
Est SE df LL UL
Comparison 3.000 0.596 9.000 1.651 4.349
$L2
Confidence Interval for the Mean Difference
Est SE df LL UL
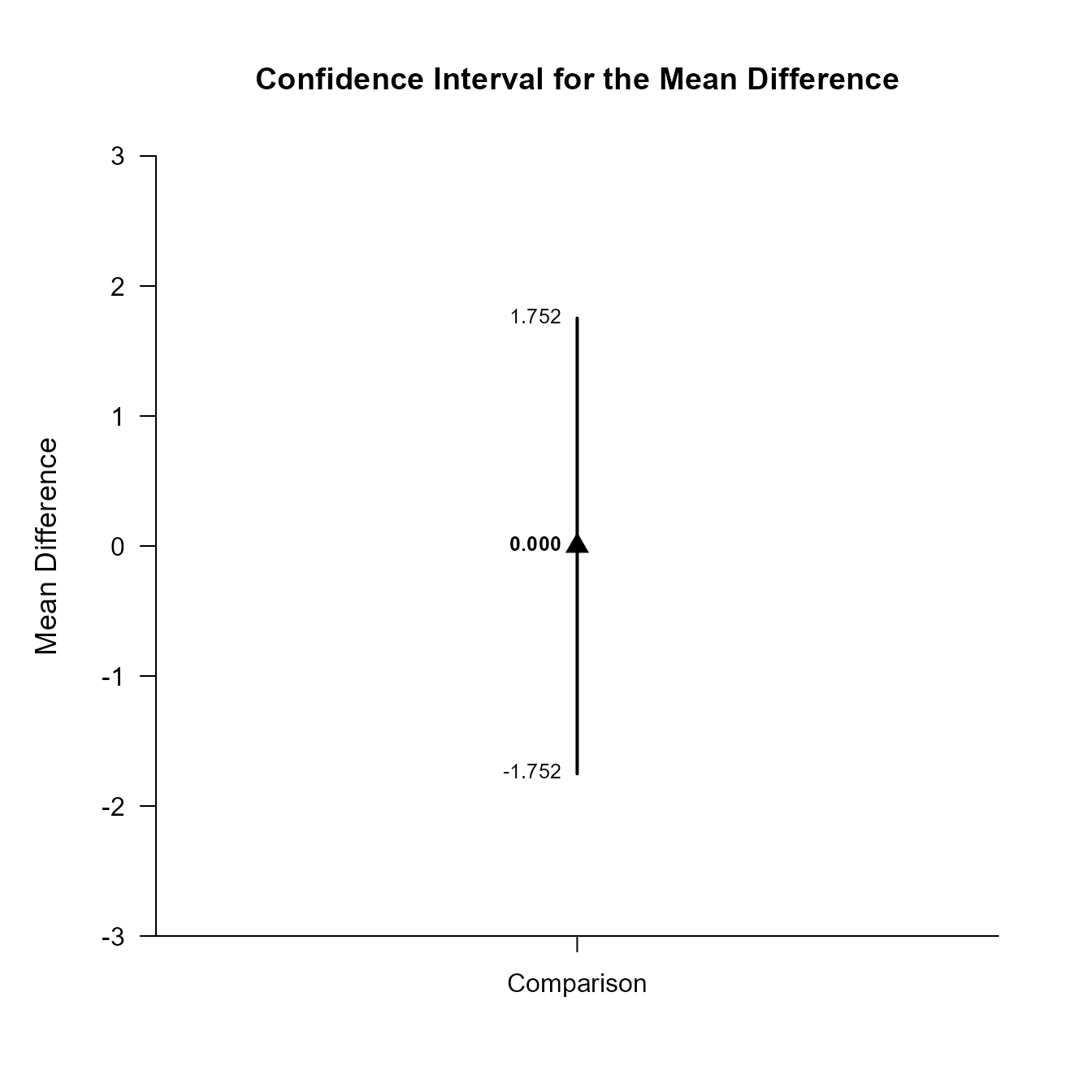
Comparison 0.000 0.775 9.000 -1.752 1.752This code obtains and plots the confidence intervals for the mean difference in the identified comparison.
(MixedMoments) |> focus(Outcome1, Outcome2) |> plotDifference(MixedCorrs)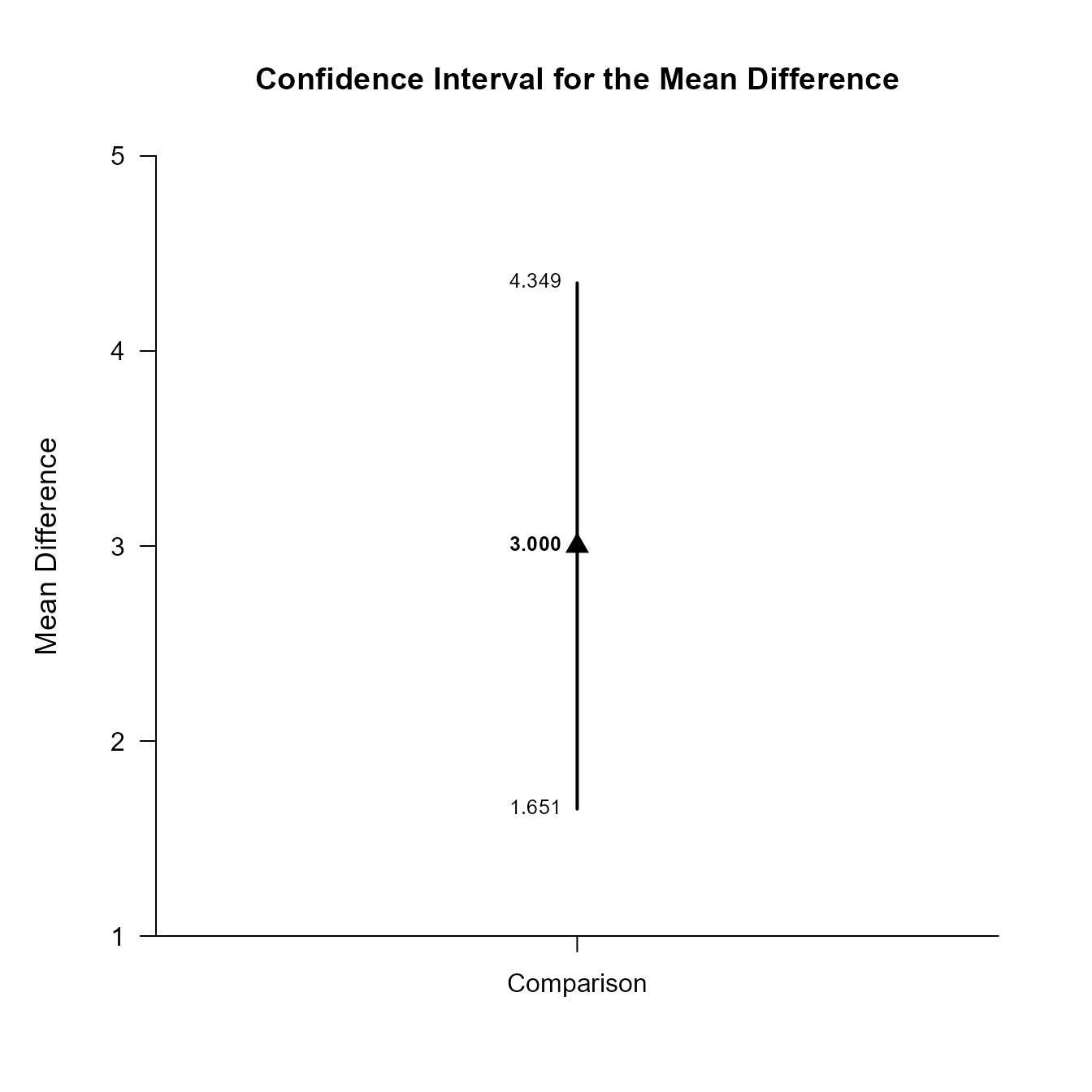
Of course, you can change the confidence level from the default 95% if desired.
(MixedMoments) |> focus(Outcome1, Outcome2) |> estimateDifference(MixedCorrs, conf.level = .99)$L1
Confidence Interval for the Mean Difference
Est SE df LL UL
Comparison 3.000 0.596 9.000 1.062 4.938
$L2
Confidence Interval for the Mean Difference
Est SE df LL UL
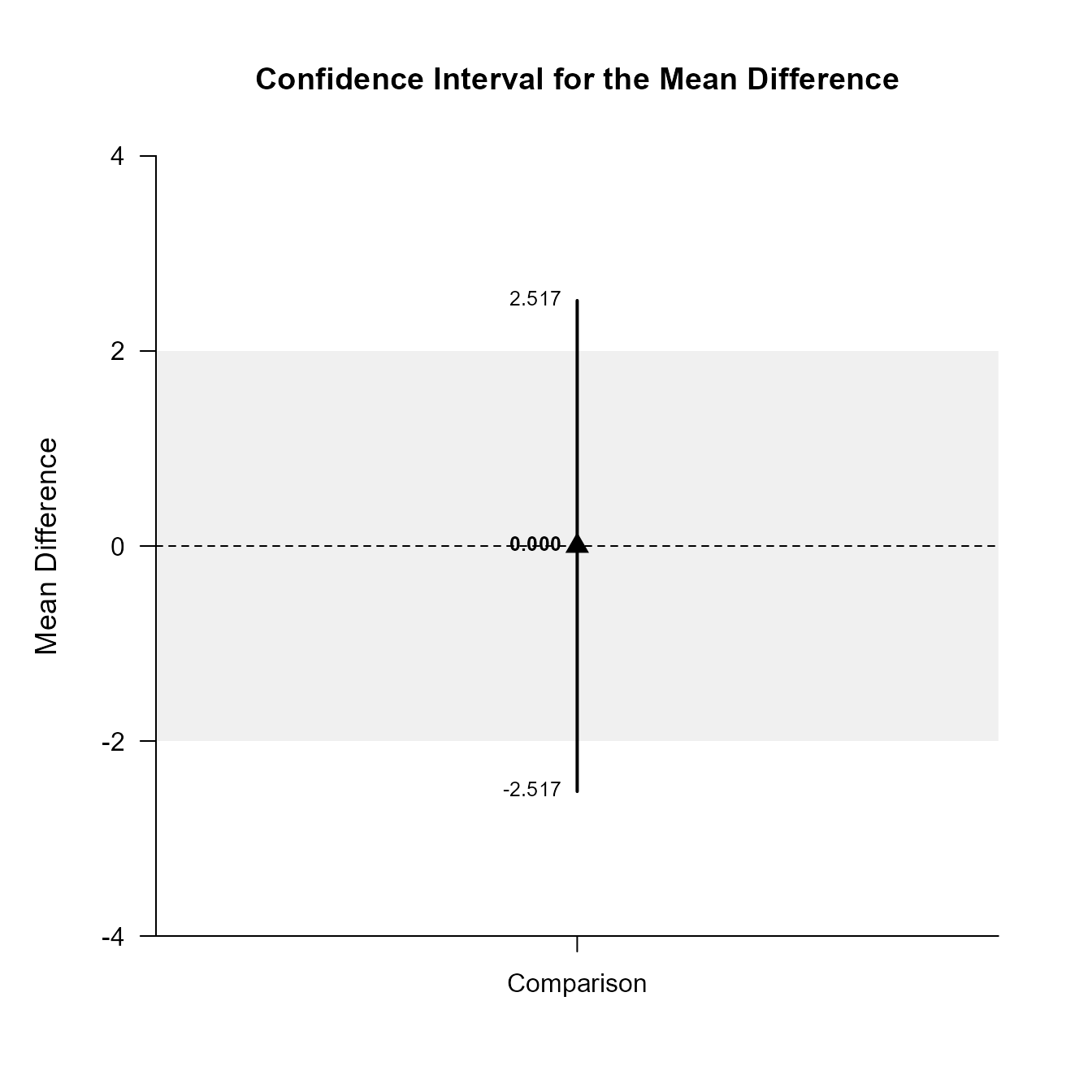
Comparison 0.000 0.775 9.000 -2.517 2.517Once again, the confidence levels can be changed away from the default and a comparison line to represent a population (or test) value and a region of practical equivalence can be added to the graph.
(MixedMoments) |> focus(Outcome1, Outcome2) |> plotDifference(MixedCorrs, conf.level = .99, line = 0, rope = c(-2, 2))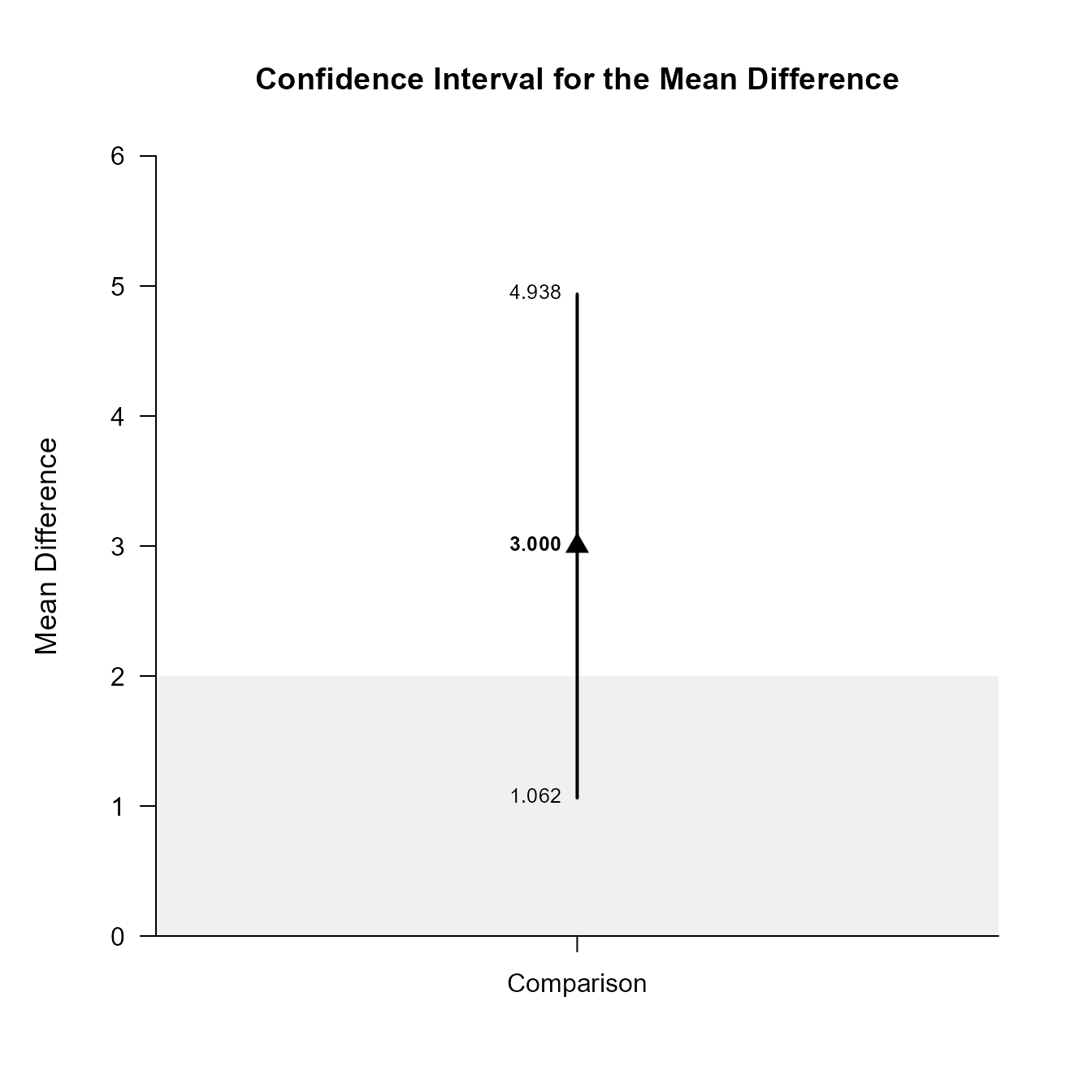
If you wish, you can get the confidence intervals for the means and the mean difference in one command.
(MixedMoments) |> focus(Outcome1, Outcome2) |> estimateComparison(MixedCorrs)$L1
Confidence Intervals for the Mean Comparison
Est SE df LL UL
Outcome1 8.000 0.447 9.000 6.988 9.012
Outcome2 11.000 0.699 9.000 9.418 12.582
Comparison 3.000 0.596 9.000 1.651 4.349
$L2
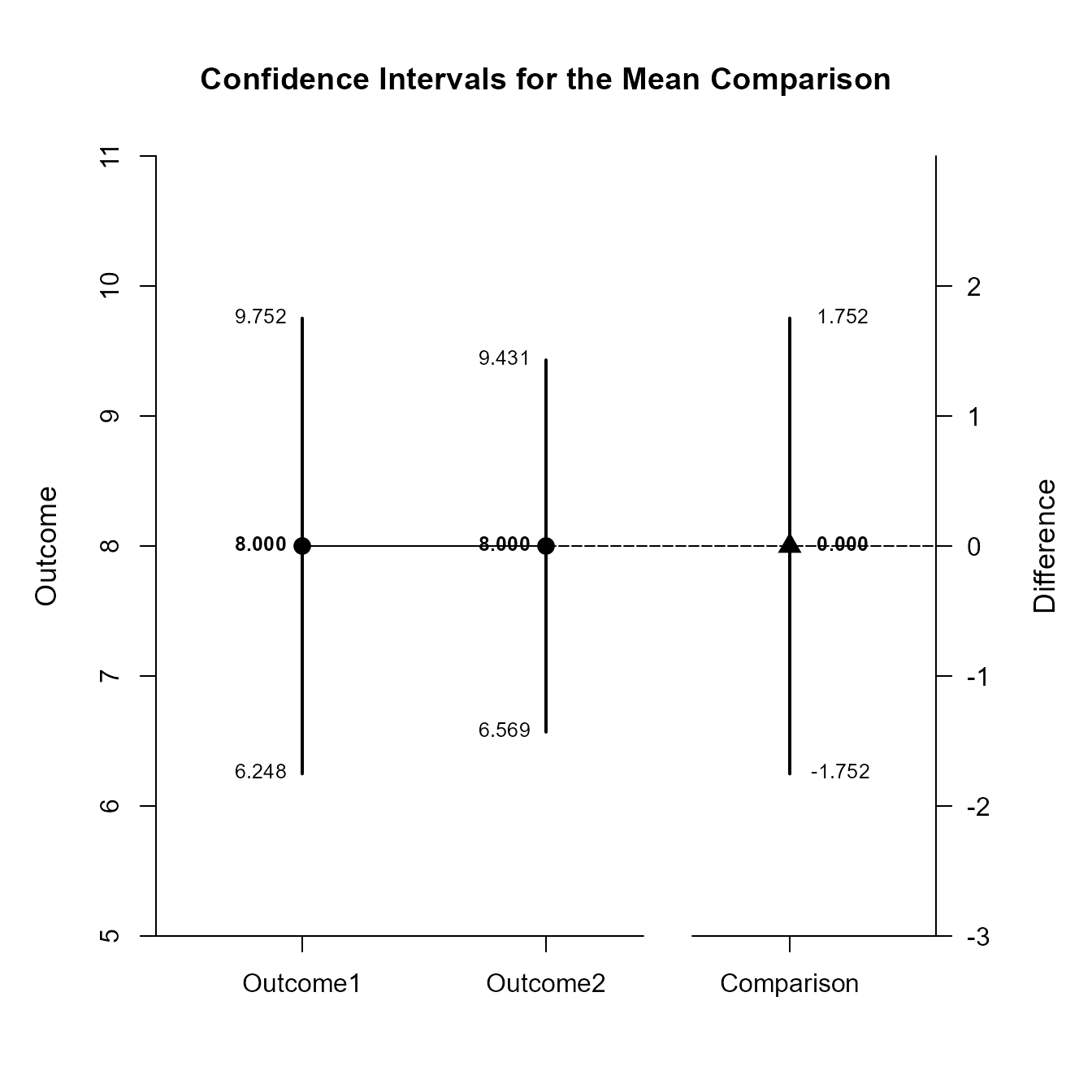
Confidence Intervals for the Mean Comparison
Est SE df LL UL
Outcome1 8.000 0.774 9.000 6.248 9.752
Outcome2 8.000 0.632 9.000 6.569 9.431
Comparison 0.000 0.775 9.000 -1.752 1.752This code produces a difference plot using the confidence intervals for the means and the mean difference.
(MixedMoments) |> focus(Outcome1, Outcome2) |> plotComparison(MixedCorrs)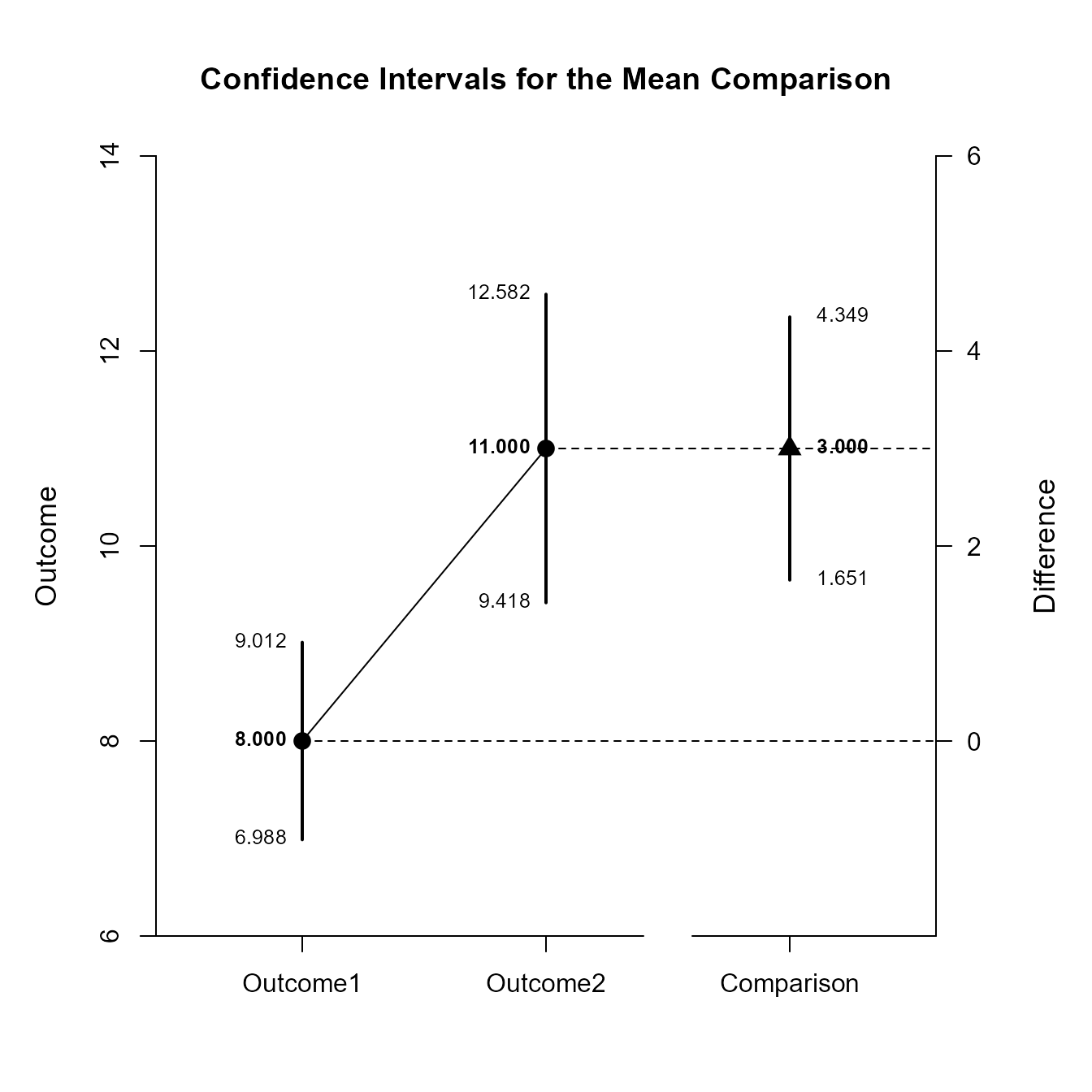
Of course, you can change the confidence level from the default 95% if desired.
(MixedMoments) |> focus(Outcome1, Outcome2) |> estimateComparison(MixedCorrs, conf.level = .99)$L1
Confidence Intervals for the Mean Comparison
Est SE df LL UL
Outcome1 8.000 0.447 9.000 6.547 9.453
Outcome2 11.000 0.699 9.000 8.728 13.272
Comparison 3.000 0.596 9.000 1.062 4.938
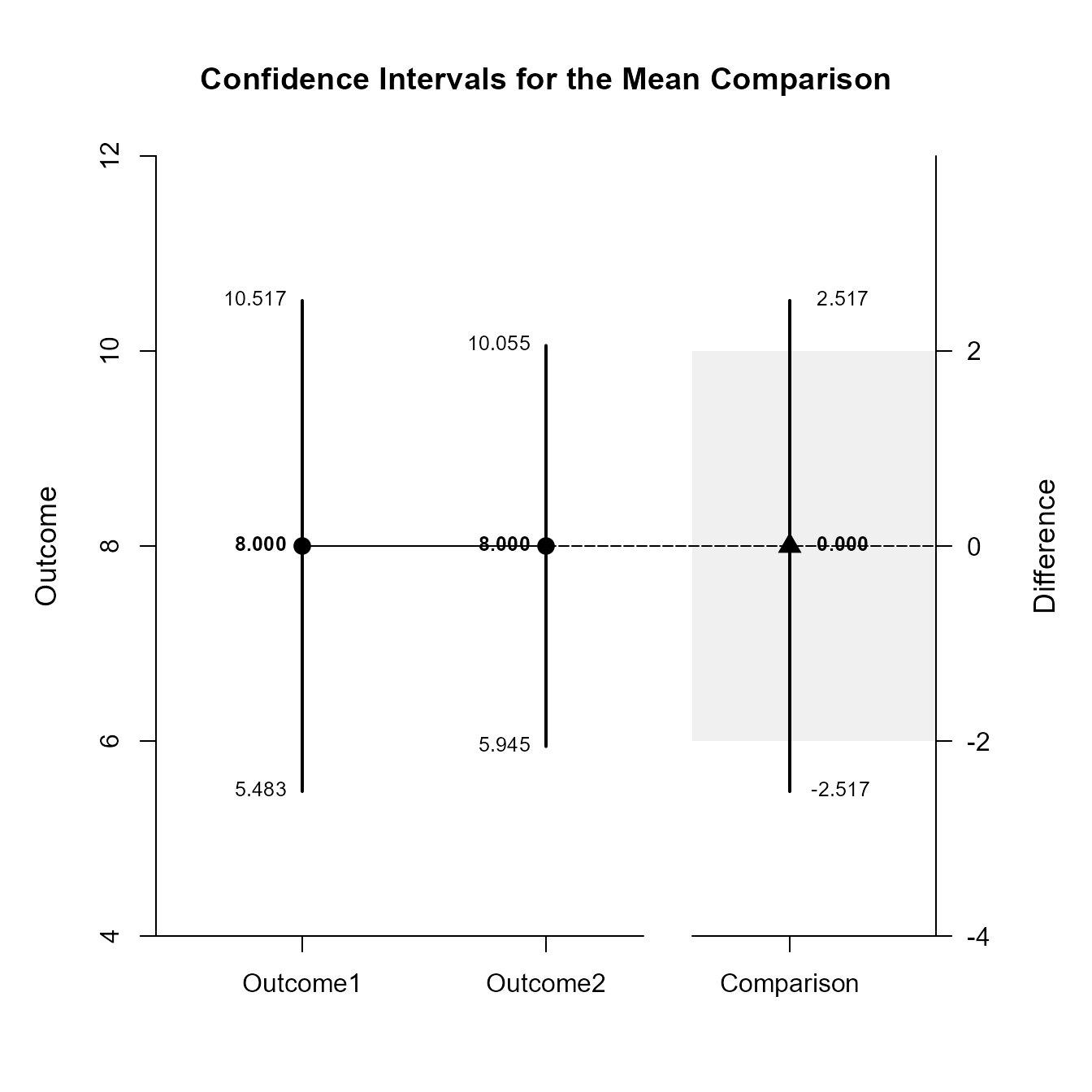
$L2
Confidence Intervals for the Mean Comparison
Est SE df LL UL
Outcome1 8.000 0.774 9.000 5.483 10.517
Outcome2 8.000 0.632 9.000 5.945 10.055
Comparison 0.000 0.775 9.000 -2.517 2.517Once again, the confidence levels can be changed away from the default and a region of practical equivalence can be added to the graph.
(MixedMoments) |> focus(Outcome1, Outcome2) |> plotComparison(MixedCorrs, conf.level = .99, rope = c(-2, 2))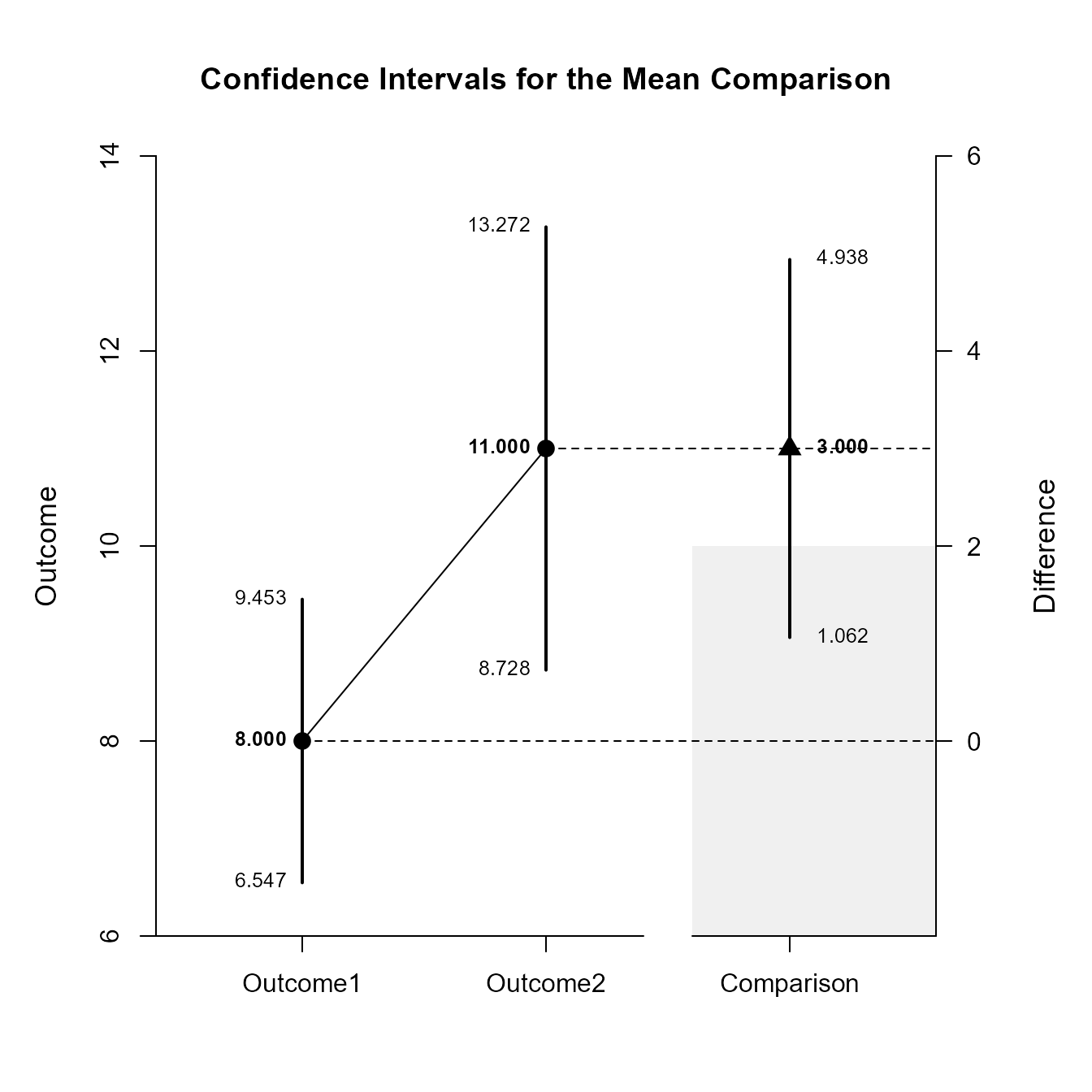
Significance Tests
This code produces NHST for the identified comparison (using a default test value of zero).
(MixedMoments) |> focus(Outcome1, Outcome2) |> testDifference(MixedCorrs)$L1
Hypothesis Test for the Mean Difference
Diff SE df t p
Comparison 3.000 0.596 9.000 5.031 0.001
$L2
Hypothesis Test for the Mean Difference
Diff SE df t p
Comparison 0.000 0.775 9.000 0.000 1.000If the default value of zero is not plausible, it too can be changed.
(MixedMoments) |> focus(Outcome1, Outcome2) |> testDifference(MixedCorrs, mu = -2)$L1
Hypothesis Test for the Mean Difference
Diff SE df t p
Comparison 5.000 0.596 9.000 8.386 0.000
$L2
Hypothesis Test for the Mean Difference
Diff SE df t p
Comparison 2.000 0.775 9.000 2.582 0.030Standardized Effect Sizes
This code calculates a standardized mean difference for the comparison and its confidence interval.
(MixedMoments) |> focus(Outcome1, Outcome2) |> standardizeDifference(MixedCorrs)$L1
Confidence Interval for the Standardized Mean Difference
d SE LL UL
Comparison 1.617 0.466 0.703 2.530
$L2
Confidence Interval for the Standardized Mean Difference
d SE LL UL
Comparison 0.000 0.365 -0.716 0.716The width of the confidence interval for the effect size can be altered if desired.
(MixedMoments) |> focus(Outcome1, Outcome2) |> standardizeDifference(MixedCorrs, conf.level = .99)$L1
Confidence Interval for the Standardized Mean Difference
d SE LL UL
Comparison 1.617 0.466 0.416 2.817
$L2
Confidence Interval for the Standardized Mean Difference
d SE LL UL
Comparison 0.000 0.365 -0.941 0.941Analyses of a Contrast
This section produces analyses involving multiple levels of a factor.
Confidence Intervals
This code produces a confidence interval for a specified contrast.
(MixedMoments) |> estimateContrast(MixedCorrs, contrast = c(-1, .5, .5))$L1
Confidence Interval for the Mean Contrast
Est SE df LL UL
Contrast 3.500 0.572 9.000 2.205 4.795
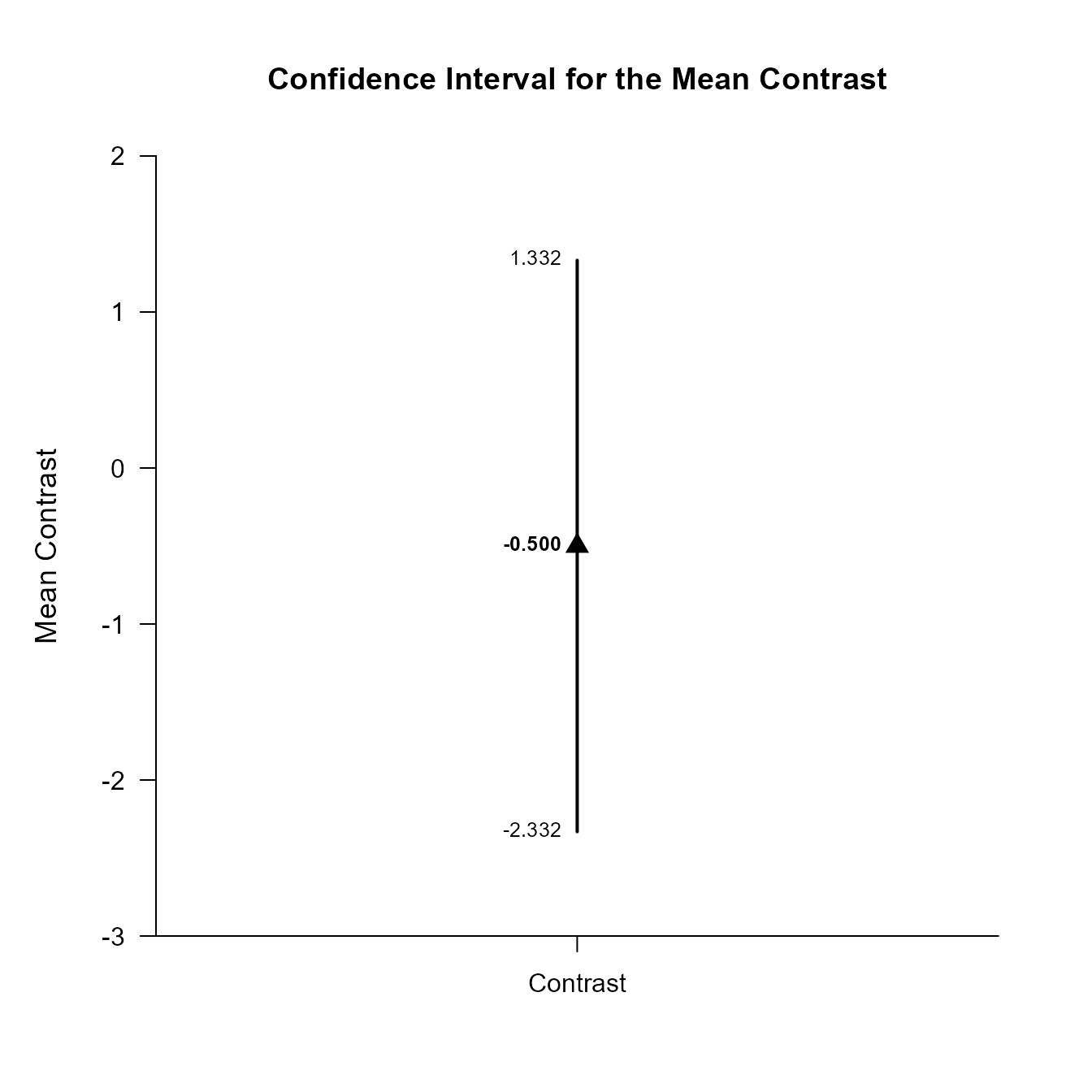
$L2
Confidence Interval for the Mean Contrast
Est SE df LL UL
Contrast -0.500 0.810 9.000 -2.332 1.332This code obtains and plots the confidence intervals for the mean difference in the identified contrast.
(MixedMoments) |> plotContrast(MixedCorrs, contrast = c(-1, .5, .5))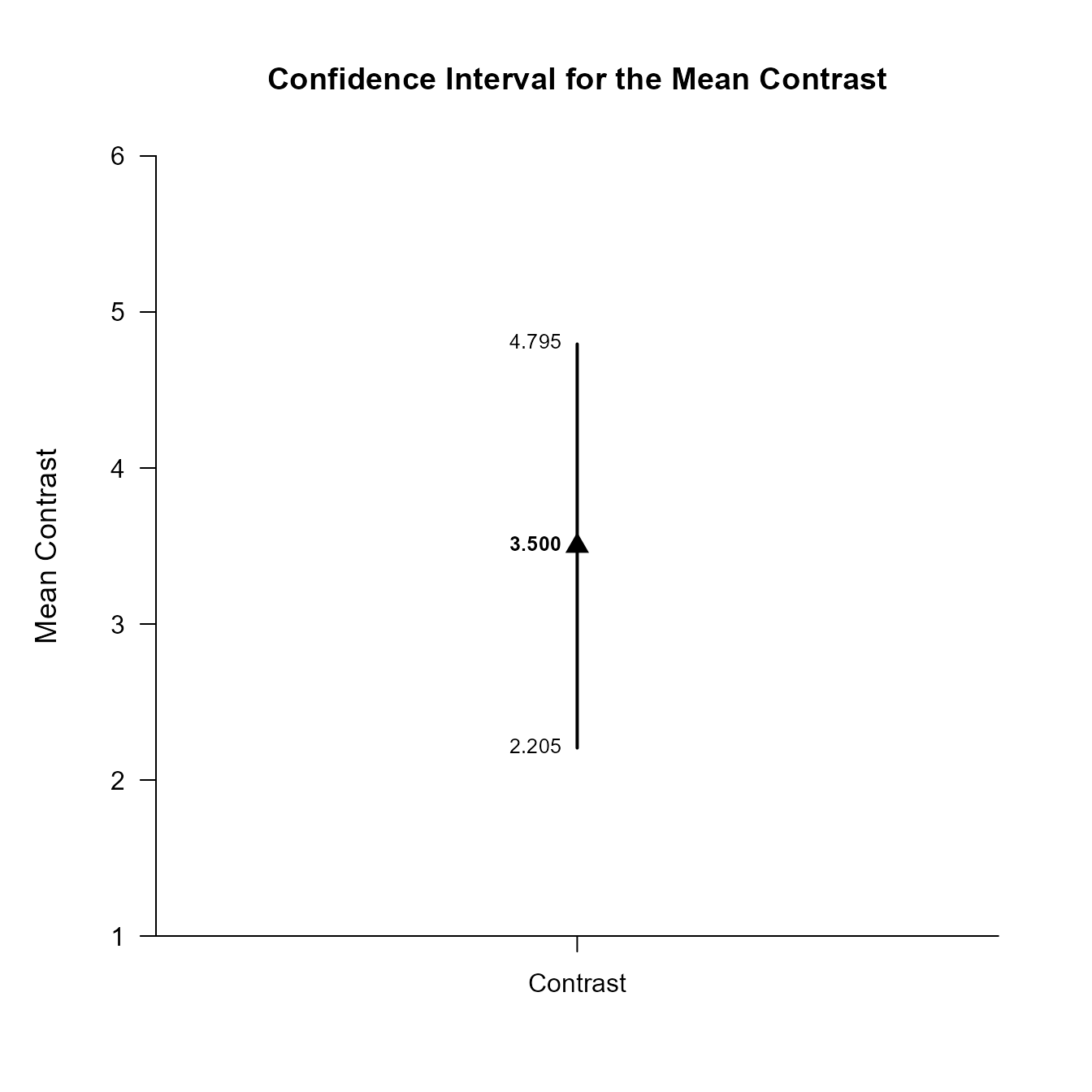
As in all other cases, the default value of the confidence interval can be changed.
(MixedMoments) |> estimateContrast(MixedCorrs, contrast = c(-1, .5, .5), conf.level = .99)$L1
Confidence Interval for the Mean Contrast
Est SE df LL UL
Contrast 3.500 0.572 9.000 1.640 5.360
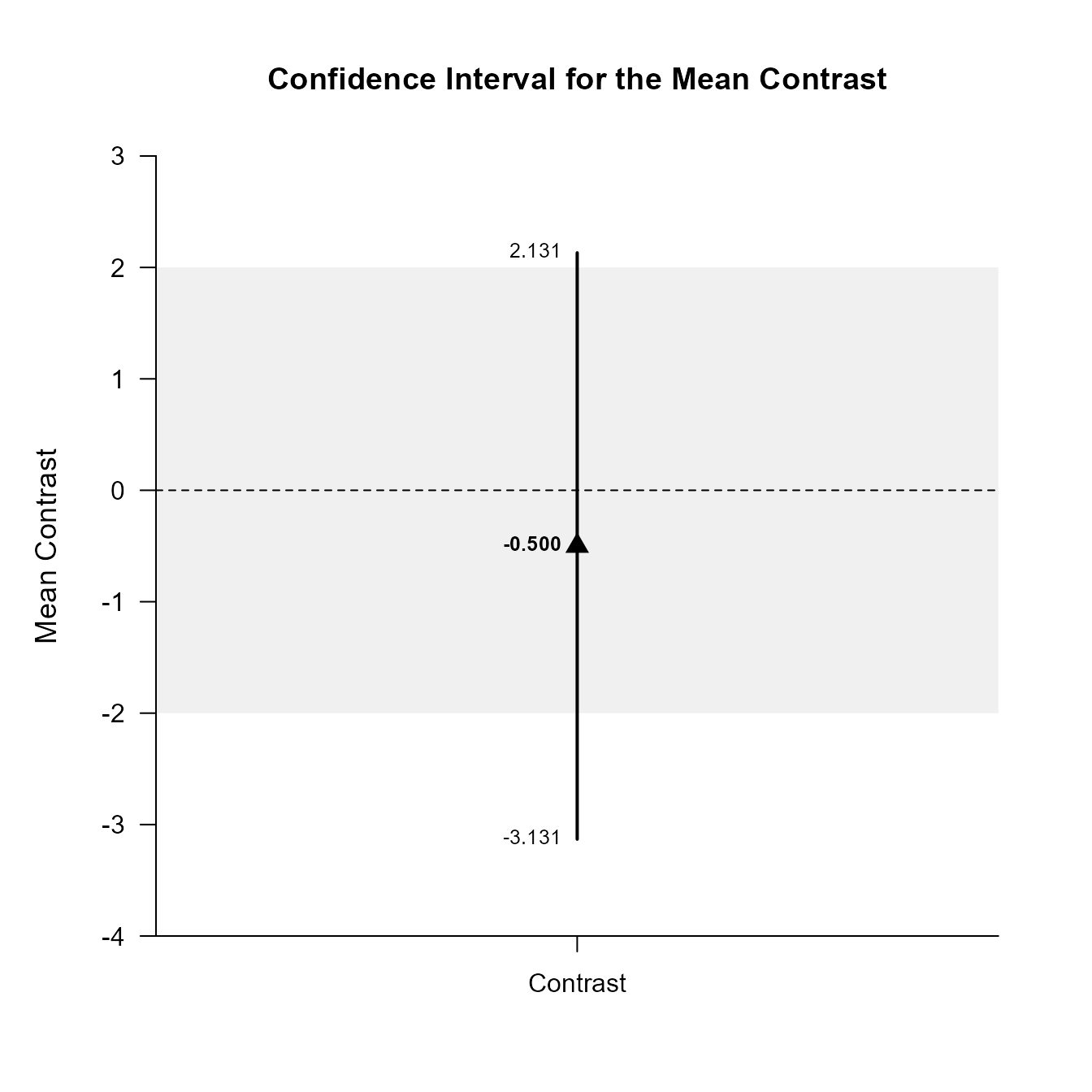
$L2
Confidence Interval for the Mean Contrast
Est SE df LL UL
Contrast -0.500 0.810 9.000 -3.131 2.131The width of the confidence interval for the contrast can be altered and a comparison line to represent a population (or test) value and a region of practical equivalence can be added to the graph.
(MixedMoments) |> plotContrast(MixedCorrs, contrast = c(-1, .5, .5), conf.level = .99, line = 0, rope = c(-2, 2))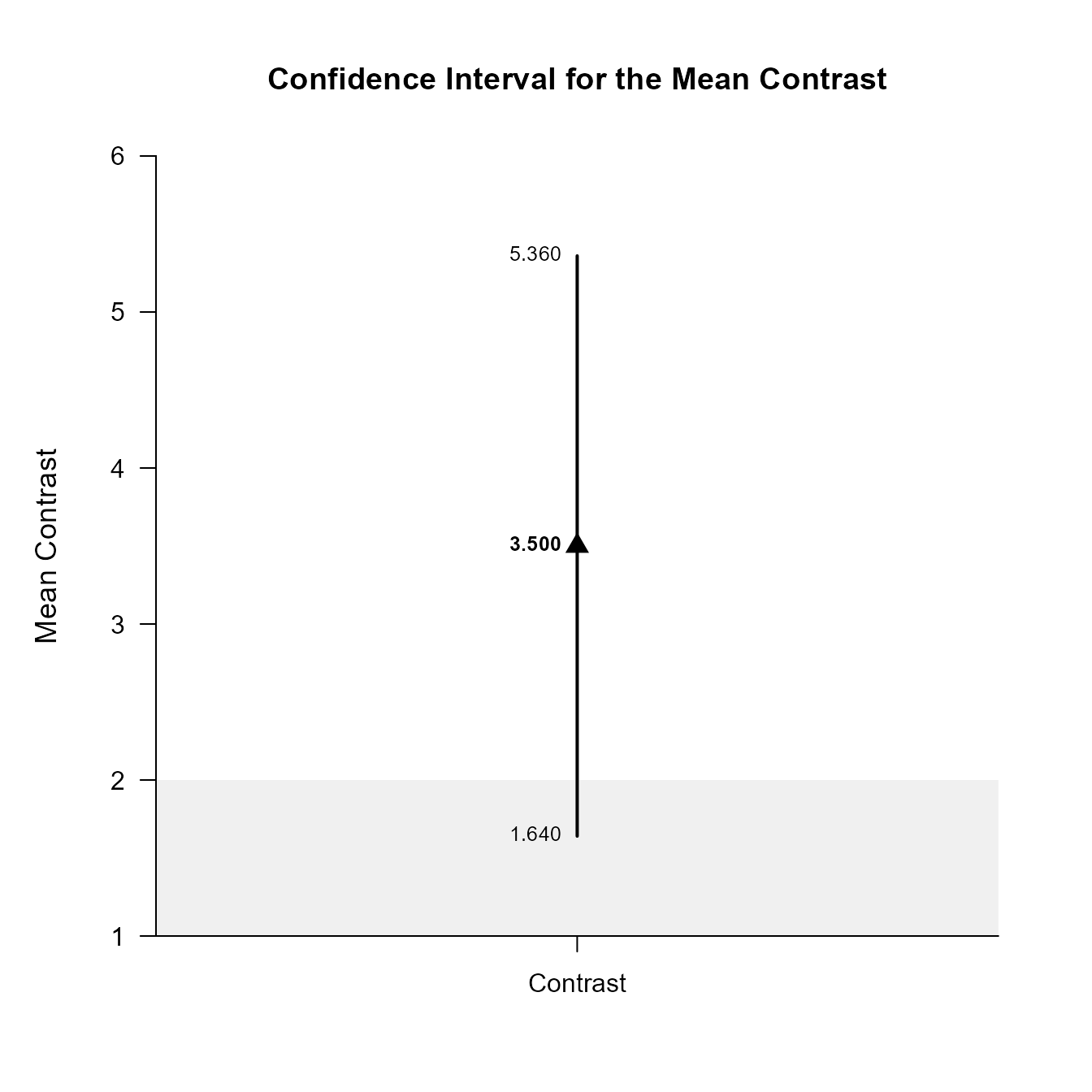
If you wish, you can get the confidence intervals for the mean subsets and the mean contrast in one command.
(MixedMoments) |> estimateSubsets(MixedCorrs, contrast = c(-1, .5, .5))$L1
Confidence Intervals for the Mean Subsets
Est SE df LL UL
Neg Weighted 8.000 0.447 9.000 6.988 9.012
Pos Weighted 11.500 0.654 9.000 10.021 12.979
Contrast 3.500 0.572 9.000 2.205 4.795
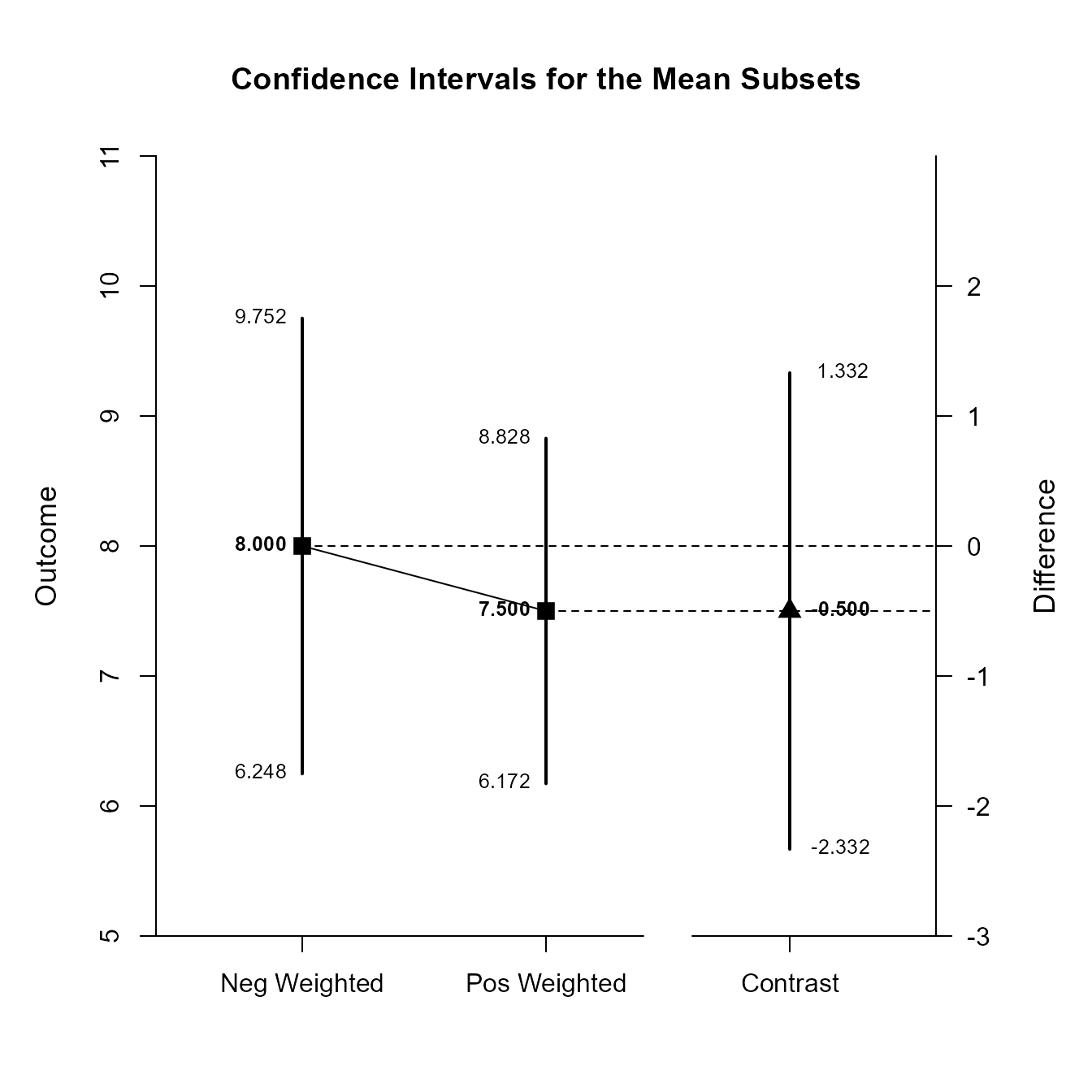
$L2
Confidence Intervals for the Mean Subsets
Est SE df LL UL
Neg Weighted 8.000 0.774 9.000 6.248 9.752
Pos Weighted 7.500 0.587 9.000 6.172 8.828
Contrast -0.500 0.810 9.000 -2.332 1.332This code produces a difference plot using the confidence intervals for the mean subsets and the mean contrast.
(MixedMoments) |> plotSubsets(MixedCorrs, contrast = c(-1, .5, .5))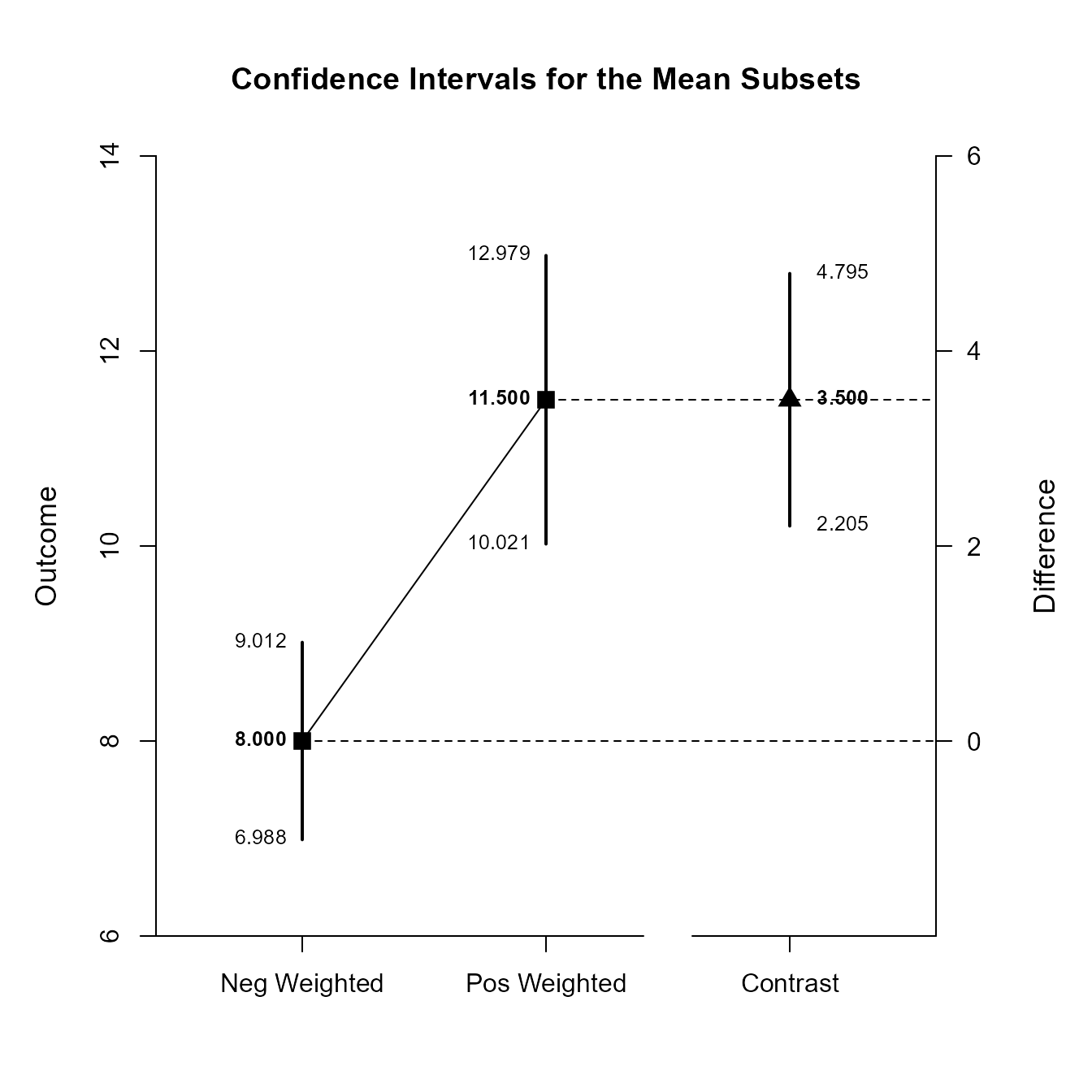
Of course, you can change the confidence level from the default 95% if desired.
(MixedMoments) |> estimateSubsets(MixedCorrs, contrast = c(-1, .5, .5), conf.level = .99)$L1
Confidence Intervals for the Mean Subsets
Est SE df LL UL
Neg Weighted 8.000 0.447 9.000 6.547 9.453
Pos Weighted 11.500 0.654 9.000 9.375 13.625
Contrast 3.500 0.572 9.000 1.640 5.360
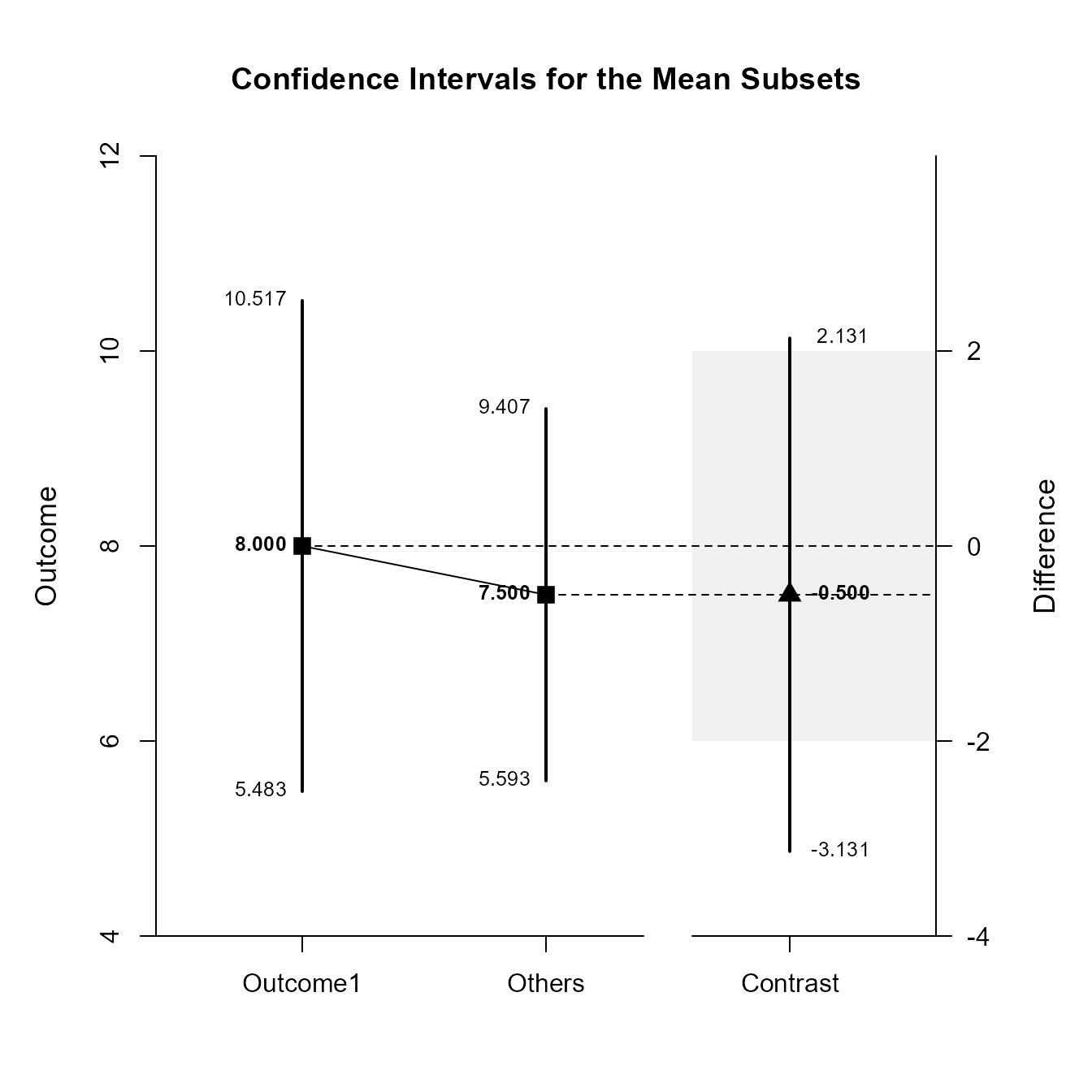
$L2
Confidence Intervals for the Mean Subsets
Est SE df LL UL
Neg Weighted 8.000 0.774 9.000 5.483 10.517
Pos Weighted 7.500 0.587 9.000 5.593 9.407
Contrast -0.500 0.810 9.000 -3.131 2.131Once again, the confidence levels can be changed away from the default and a region of practical equivalence can be added to the graph.
(MixedMoments) |> plotSubsets(MixedCorrs, contrast = c(-1, .5, .5), labels = c("Outcome1", "Others"), conf.level = .99, rope = c(-2, 2))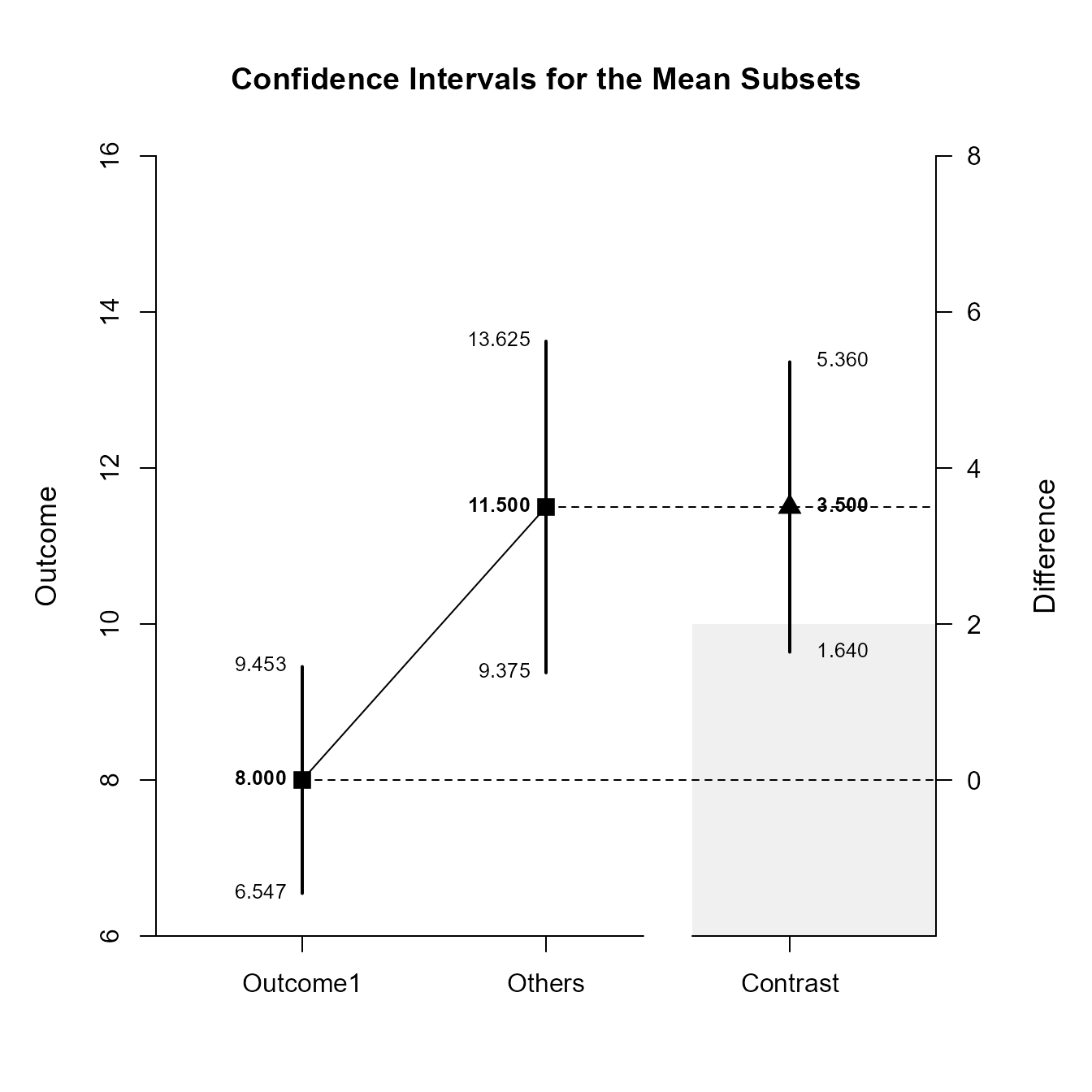
Significance Tests
This code produces a NHST for the identified contrast. It tests the contrast against a value of zero default.
(MixedMoments) |> testContrast(MixedCorrs, contrast = c(-1, .5, .5))$L1
Hypothesis Test for the Mean Contrast
Est SE df t p
Contrast 3.500 0.572 9.000 6.116 0.000
$L2
Hypothesis Test for the Mean Contrast
Est SE df t p
Contrast -0.500 0.810 9.000 -0.618 0.552If desired, the contrast can be tested against other values.
(MixedMoments) |> testContrast(MixedCorrs, contrast = c(-1, .5, .5), mu = 4)$L1
Hypothesis Test for the Mean Contrast
Est SE df t p
Contrast -0.500 0.572 9.000 -0.874 0.405
$L2
Hypothesis Test for the Mean Contrast
Est SE df t p
Contrast -4.500 0.810 9.000 -5.558 0.000Standardized Effect Sizes
This code calculates a standardized contrast and its confidence interval.
(MixedMoments) |> standardizeContrast(MixedCorrs, contrast = c(-1, .5, .5))$L1
Confidence Interval for the Standardized Mean Contrast
Est SE LL UL
Contrast 1.689 0.371 0.962 2.415
$L2
Confidence Interval for the Standardized Mean Contrast
Est SE LL UL
Contrast -0.224 0.341 -0.892 0.443The width of the confidence interval for the effect size can be altered if desired.
(MixedMoments) |> standardizeContrast(MixedCorrs, contrast = c(-1, .5, .5), conf.level = .99)$L1
Confidence Interval for the Standardized Mean Contrast
Est SE LL UL
Contrast 1.689 0.371 0.734 2.644
$L2
Confidence Interval for the Standardized Mean Contrast
Est SE LL UL
Contrast -0.224 0.341 -1.102 0.653Analyses of 2x2 Interaction Comparisons
This section produces analyses involving an interaction among multiple factors.
Confidence Intervals
Identify a 2 x 2 interaction of interest (in this case, two levels of Outcome and the existing two levels of the Factor). Estimate and plot the interaction contrast (which includes the comparisons within each simple effect).
(MixedMoments) |> focus(Outcome1, Outcome2) |> estimateInteraction(MixedCorrs)
Confidence Intervals for the Mean Interaction
Est SE df LL UL
Simple Effect at L1 3.000 0.596 9.000 1.651 4.349
Simple Effect at L2 0.000 0.775 9.000 -1.752 1.752
Interaction -3.000 0.978 16.894 -5.063 -0.937
(MixedMoments) |> focus(Outcome1, Outcome2) |> plotInteraction(MixedCorrs)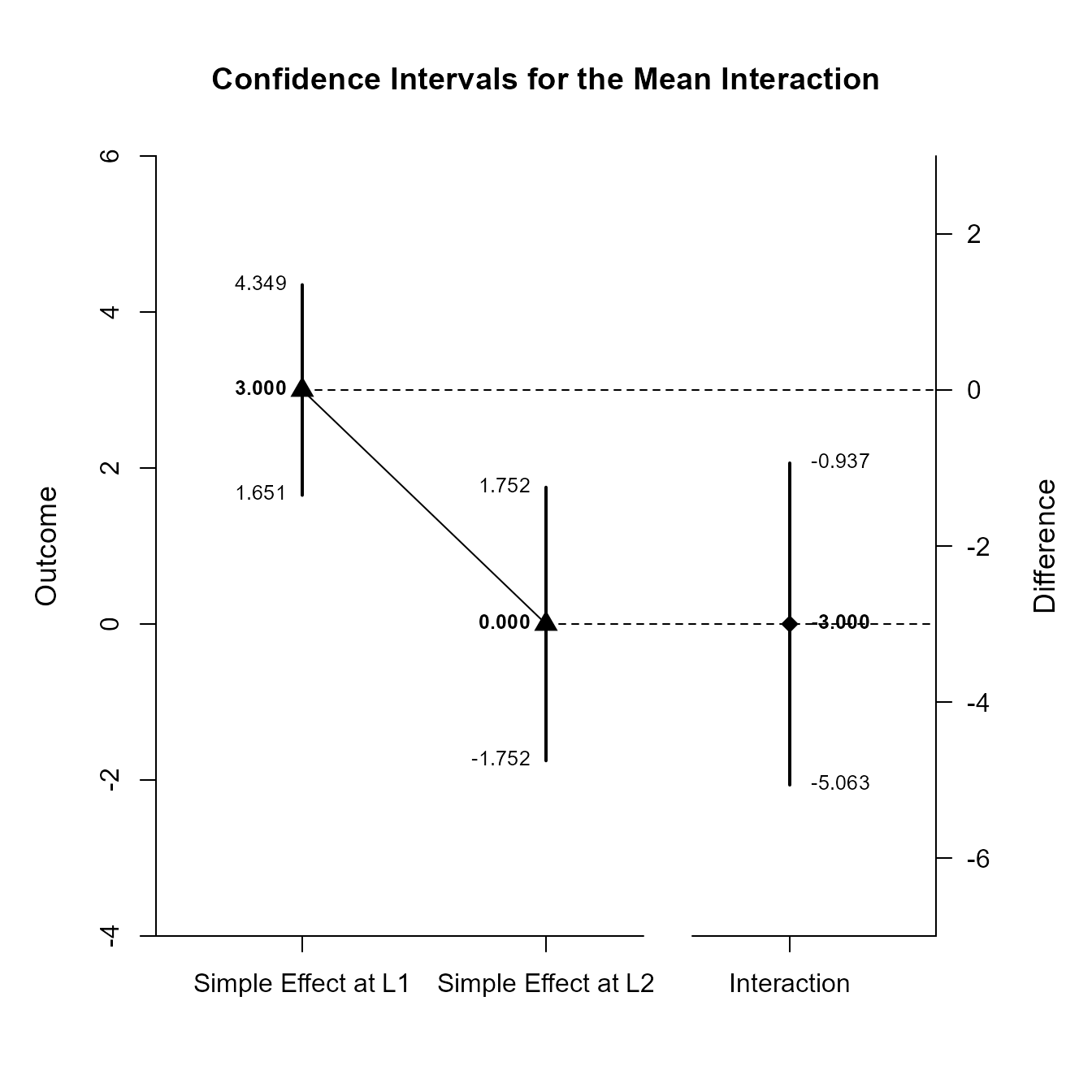
Significance Tests
Test the interaction contrast (which includes the comparisons within each simple effect) for statistical significance.
(MixedMoments) |> focus(Outcome1, Outcome2) |> testInteraction(MixedCorrs)
Hypothesis Tests for the Mean Interaction
Est SE t df p
Effect at L1 3.000 0.596 9.000 5.031 0.001
Effect at L2 0.000 0.775 9.000 0.000 1.000
Interaction -3.000 0.978 -3.069 16.894 0.007