Factorial Data Traditional
Source:vignettes/FactorialDataTraditional.Rmd
FactorialDataTraditional.RmdThis page examines a two-factor between-subjects (factorial) design using raw data input, focusing on omnibus and simple effects analyses.
Preliminary Tasks
Data Entry
This code inputs the variable names and creates a viewable data frame.
FactorA <- c(rep(1, 20), rep(2, 20), rep(3, 20))
FactorA <- factor(FactorA, levels = c(1, 2, 3), labels = c("A1", "A2", "A3"))
FactorB <- c(rep(1, 10), rep(2, 10), rep(1, 10), rep(2, 10), rep(1, 10), rep(2, 10))
FactorB <- factor(FactorB, levels = c(1, 2), labels = c("B1", "B2"))
Outcome <- c(6, 8, 6, 8, 10, 8, 10, 9, 8, 7, 5, 9, 10, 9, 11, 4, 11, 7, 6, 8, 7, 13, 11, 10, 13, 8, 11, 14, 12, 11, 7, 8, 7, 11, 10, 7, 8, 4, 8, 10, 9, 16, 11, 12, 15, 13, 9, 14, 11, 10, 8, 6, 8, 11, 5, 7, 9, 3, 6, 7)
FactorialData <- construct(FactorA, FactorB, Outcome)Summary Statistics
This code provides a table of summary statistics.
(Outcome ~ FactorA) |> describeMoments(by = FactorB)$B1
Summary Statistics for the Data
N M SD Skew Kurt
A1 10.000 8.000 1.414 0.000 -0.738
A2 10.000 11.000 2.211 -0.617 -0.212
A3 10.000 12.000 2.449 0.340 -1.102
$B2
Summary Statistics for the Data
N M SD Skew Kurt
A1 10.000 8.000 2.449 -0.340 -1.102
A2 10.000 8.000 2.000 -0.417 0.735
A3 10.000 7.000 2.211 0.000 0.665Plot the means and their confidence intervals for the design as a whole.
(Outcome ~ FactorA) |> plotFactorial(by = FactorB, col = c("darkred", "darkblue"))
legend("topleft", inset = .01, box.lty = 0, pch = 16, legend = c("B1", "B2"), col = c("darkred", "darkblue"))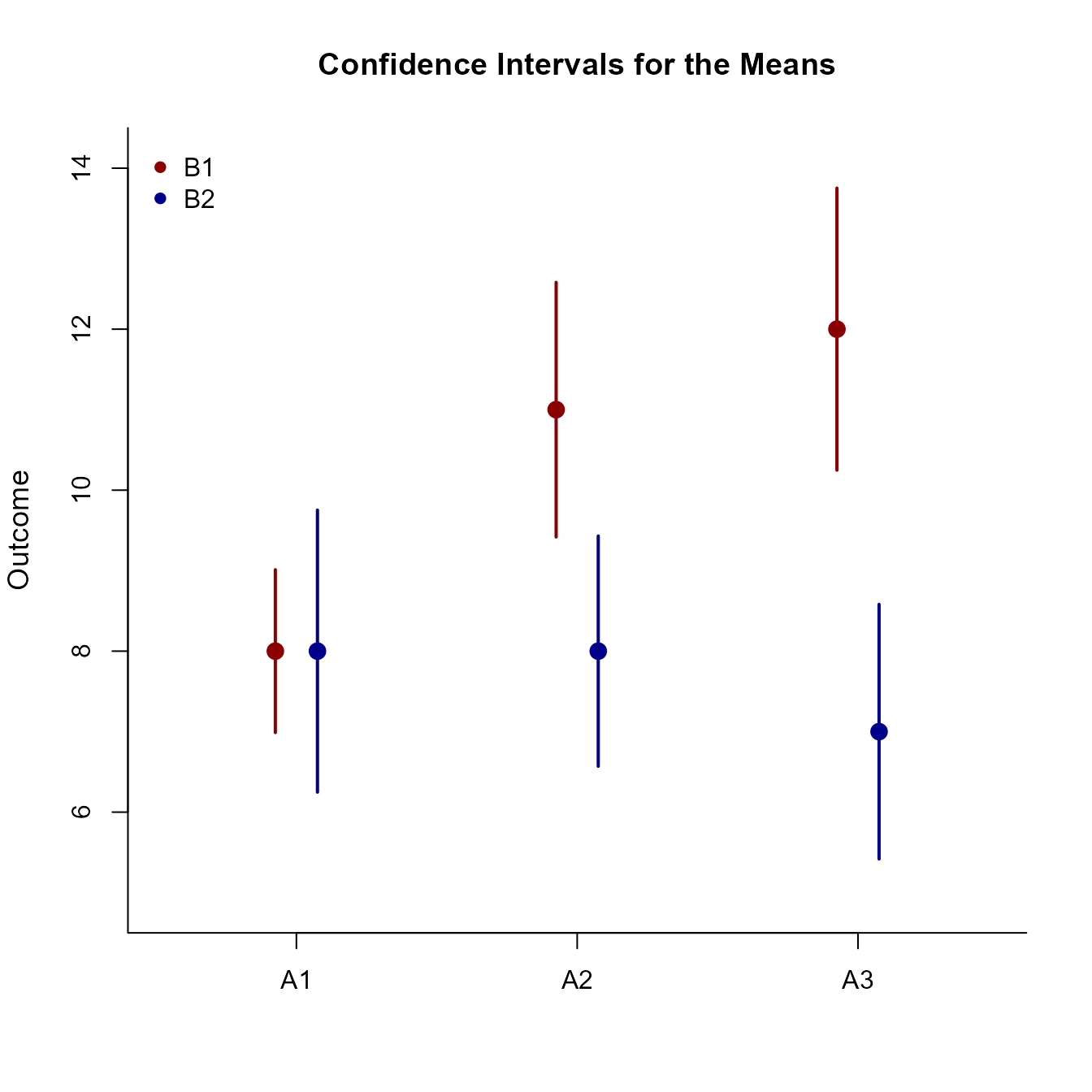
Analyses of the Omnibus Effects
The omnibus analysis usually consists of an Analysis of Variance.
Source Table
Get the source table associated with the main effects and the interaction.
(Outcome ~ FactorA) |> describeFactorial(by = FactorB)
Source Table for the Model
SS df MS
Factor 106.667 1.000 106.667
Blocks 30.000 2.000 15.000
Factor:Blocks 63.333 2.000 31.667
Residual 250.000 54.000 4.630Proportion of Variance Accounted For
Get estimates of the proportion of variance accounted for by each effect (along with their confidence intervals).
(Outcome ~ FactorA) |> estimateFactorial(by = FactorB)
Proportion of Variance Accounted For by the Model
Est LL UL
Factor 0.299 0.136 0.437
Blocks 0.107 0.000 0.176
Factor:Blocks 0.202 0.014 0.248Significance Tests
Finally, test the various effects for statistical significance.
(Outcome ~ FactorA) |> testFactorial(by = FactorB)
Hypothesis Tests for the Model
F df1 df2 p
Factor 23.040 1.000 54.000 0.000
Blocks 3.240 2.000 54.000 0.047
Factor:Blocks 6.840 2.000 54.000 0.002Analyses of the Simple Effects
As a follow-up to an Analysis of Variance, it is cusotmary to examine the simple effects (essentially a single-factor ANOVA separately across the levels of another factor).
Source Table
Get the source tables separately for the simple effects.
(Outcome ~ FactorA) |> describeMoments(by = FactorB) |> describeEffect()$B1
Source Table for the Model
SS df MS
Between 86.667 2.000 43.333
Within 116.000 27.000 4.296
$B2
Source Table for the Model
SS df MS
Between 6.667 2.000 3.333
Within 134.000 27.000 4.963Proportion of Variance Accounted For
Get an estimate of the proportion of variance account for by the simple effect (and the confidence interval for that estimate).
(Outcome ~ FactorA) |> describeMoments(by = FactorB) |> estimateEffect()$B1
Proportion of Variance Accounted For by the Model
Est LL UL
Factor 0.428 0.157 0.569
$B2
Proportion of Variance Accounted For by the Model
Est LL UL
Factor 0.047 0.000 0.173Significance Tests
Finally, test the simple effects for statistical significance.
(Outcome ~ FactorA) |> describeMoments(by = FactorB) |> testEffect()$B1
Hypothesis Test for the Model
F df1 df2 p
Factor 10.086 2.000 27.000 0.001
$B2
Hypothesis Test for the Model
F df1 df2 p
Factor 0.672 2.000 27.000 0.519